Fibonacci in de natuur
1. De rij van Fibonacci
Artikel van Scientias. Geschreven op 11-08-2012 door Caroline Kraaijvanger
Wiskunde en natuur komen samen als we tussen al het groen speuren naar de Rij van Fibonacci en die nog vinden ook! In zijn boek 'Liber Abaci' presenteerde Leonardo van Pisa (ook Fibonacci genoemd) in de dertiende eeuw een bijzondere rij cijfers. De rij is tegenwoordig beter bekend als de Rij van Fibonacci. Hoewel de naam doet vermoeden dat hij de rij ontdekte, is dat onterecht. In India waren wiskundigen al veel eerder op de bijzondere rij gestuit.
De rij
De Rij van Fibonacci ziet er als volgt uit (zie hieronder). De rij wordt verkregen door de twee getallen die aan het gezochte getal x voorafgaan, bij elkaar op te tellen. Dus: 2 en 3 maakt 5, 3 en 5 maakt 8, 5 en 8 maakt 13, enzovoort.
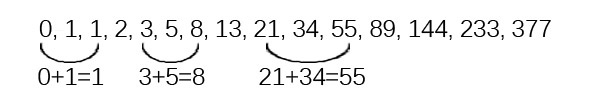
Natuur
Opvallend genoeg is de Rij van Fibonacci niet alleen in wiskundelokalen terug te vinden. Ook in de natuur treffen we de rij aan. Tijd voor enkele voorbeelden.
Wilde bertram
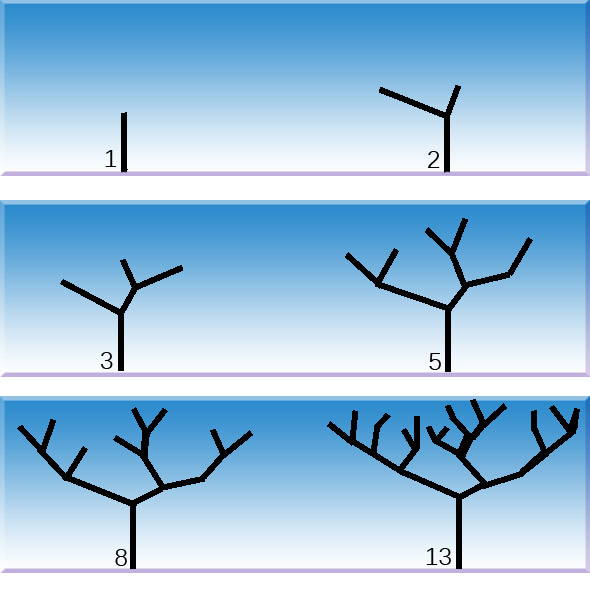
De Wilde bertram volgt de Rij van Fibonacci. Tel het aantal uiteinden maar na!
Gulden Snede
De Rij van Fibonacci benadert ook de gulden snede. De gulden snede berekent u door 1 op te tellen bij de wortel van 5 en het resultaat daarvan te delen door 2. U krijgt dan een getal dat 1,62 benadert. Wat gebeurt er nu als we de opeenvolgende cijfers in de rij van Fibonacci met elkaar delen? Kijk en reken even mee: 13/8 = 1,62; 21/13 = 1,615; 233/144 = 1,62
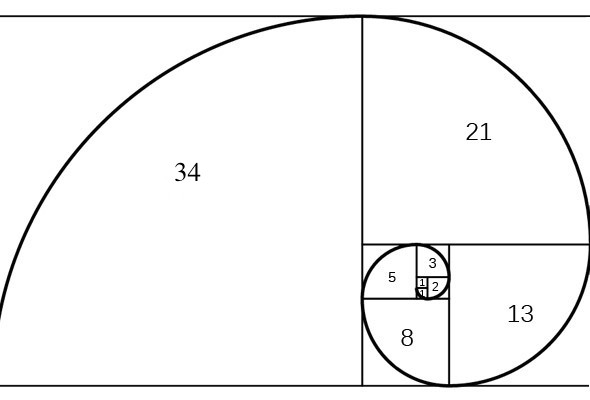
Afbeelding: Dicklyon (Wikimedia Commons).
2. Theorie over mysterieuze fibonaccipatronen in de natuur geldt niet vanaf het eerste begin.
Tien procent van de planten beantwoordt niet aan dat patroon.
Scientias, 19-06-2023, door Jeanette Kras
Van zonnebloemen en denne-appels tot broccoli en ananas, maar ook tal van bladeren: allemaal volgen ze de Rij van Fibonacci. Tot nu toe werd gedacht dat dit al sinds het begin van de evolutie zo gaat, maar nieuw onderzoek toont aan dat de vroegste planten er anders uitzagen.
Even opfrissen: de beroemde wiskundige rij, die Fibonacci al in 1202 ontdekte (hij heet officieel Leonardo van Pisa), gaat als volgt: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 enz. Het nieuwe cijfer in de rij is de optelsom van de twee voorafgaande cijfers.
Veel vormen in de natuur blijken aan deze formule te voldoen. De verklaring is minder mysterieus dan je denkt: het is in veel gevallen de nuttigste manier om dingen te rangschikken. De zonnebloem kan op deze manier bijvoorbeeld de meeste zaden op het bloembed vormen. En hoe meer zaden, hoe beter de voortplanting zal gaan. De blaadjes van planten zitten dan weer volgens het fibonacci-patroon aan de steel, omdat ze dan het meeste zonlicht opvangen. Ruim 90 procent van alle rangschikkingen die voorkomen bij bloemblaadjes, zaden of bladeren volgt het bekende spiraalvormige patroon.
Twee evolutionaire richtingen
Maar dat is niet altijd zo geweest. De bladeren van de eerste planten die op Aarde groeiden, hadden een andere rangschikking. Dit weerlegt het idee dat er één evolutionaire lijn is waarlangs planten zich hebben ontwikkeld. Dat werd altijd gedacht omdat het fibonacci-patroon zo wijdverspreid is. Maar vermoedelijk zijn er dus twee verschillende evolutionaire paden. Tot die ontdekking kwamen onderzoekers van de University of Edinburgh, nadat ze een 407 miljoen jaar oud fossiel vonden van een plant, die geen Fibonacci-spiraal had.
Met digitale reconstructietechnieken maakten de wetenschappers de eerste 3D-modellen van de bladeren van een fossiele wolfsklauw, de Asteroxylon mackiei, die tot de allereerste groep bladerrijke planten behoort. Het bijzonder goed bewaard gebleven fossiel werd gevonden op de beroemde vindplaats de Rhynie Chert, een sedimentafzetting bij het Schotse Aberdeenshire. De plek bevat bewijs van een van de eerste ecosystemen ter wereld, toen landplanten zich voor het eerst ontwikkelden en langzaam het rotsachtige oppervlak van de Aarde bedekten, waardoor de planeet leefbaar werd.
Vroeger ging het anders
Het 3D-model onthulde dat de bladeren en zaden van de fossiele wolfsklauw voornamelijk waren gerangschikt in niet-fibonacci-spiralen, die zeldzaam zijn bij moderne planten. De wetenschappers kwamen tot die conclusie door de spiralen met de klok mee en tegen de klok in te tellen. En wat viel op: het betrof steeds 7 en 8 of 4 en 5 spiralen, wat geen fibonacci-cijfers zijn. Aangezien de wolfsklauw de vroegste plantenfamilie vormt, ziet het er naar uit dat de niet-fibonacci-spiralen er eerst waren en dat daarna pas de fibonacci-bladerrangschikkingen ontstonden.
"Ons model van de Asteroxylon mackiei maakt het voor het eerst mogelijk om de rangschikking van fossiele bladeren in 3D te bestuderen. Het is ongelooflijk dat we met behulp van 3D-printen een 407 miljoen jaar oud bladfossiel in onze handen kunnen houden," zegt hoofdonderzoeker Sandy Hetherington van de University of Edinburgh. "Onze bevindingen bieden een nieuw perspectief op de evolutie van de fibonacci-spiralen in planten."
Geen gegeven
Onderzoeker Holly-Anne Turner is het met haar eens. "De wolfsklauw Asteroxylon mackiei is een van de oudste voorbeelden van een plant met bladeren in ons fossielenbestand. Door de 3D-reconstructies konden we de afzonderlijke spiralen van bladeren opsporen rond de stelen van deze honderden miljoenen jaren oude fossielen. Onze analyse van de bladrangschikking bij de wolfsklauw toont aan, dat de allereerste planten bladeren hadden die niet het spiraalvormige fibonaccipatroon volgden."
Dit zet de theorie over fibonaccispiralen in de natuur in een ander licht. Dit patroon blijkt geen gegeven te zijn in de hele evolutie, want de bladeren van de vroegste wolfsklauw hadden een andere evolutionaire geschiedenis dan de meeste hedendaagse plantenfamilies, zoals varens, coniferen of bloeiende planten.
Bron:
"Fossil study sheds light on famous spirals found in nature" - Science
Opmerking van een lezer van dit artikel:
Evolutie is een doorlopend pad van 'goed genoeg naar beter'. Wat voor reden zou er geweest kunnen zijn, dat planten meteen al op de juiste formule zouden zijn uitgekomen? Dat lijkt me juist hoogst onwaarschijnlijk. Ook bij de ontwikkeling van dieren is er voor zover we weten eerst ook een periode geweest van uitproberen (Ediacara-periode), waar de meest geschikte deelnemers als overwinnaars uit tevoorschijn kwamen.
terug naar de Gulden snede
^



