D.C. Giancoli Natuurkunde deel III, Moderne natuurkunde

Academic service den Haag 1994, ISBN 90 6233 908 5
(Opmerkingen tussen haakjes zijn van mij, Freek. De tekstgedeelten die al te diep op het onderwerp ingaan met veel wiskundige formules, heb ik er tussenuit gelaten. De belangrijke paragraaf over spectraallijnen ontbrak helaas in dit exemplaar.)

Inhoud

Hoofdstuk 40 - De speciale relativiteitstheorie
Inleiding
40-1 Relativiteit volgens Galileï en Newton
40-3 Postulaten van de speciale relativiteitstheorie
40-4 Gelijktijdigheid
40-5 Tijddilatatie en de tweelingparadox
40-6 Lengtecontractie
40-7 Vierdimensionale ruimte-tijd
40-9 Relativistische massa en impuls
40-10 De hoogst mogelijke snelheid
40-11 E = mc² - Massa en energie
40-12 De invloed van de speciale relativiteitstheorie op ons wereldbeeld
Samenvatting

Hoofdstuk 41 - De vroege quantumtheorie
Inleiding
41-1 De quantumhypothese van Planck
41-2 De theorie van lichtfotonen en het foto-elektrische effect
41-4 Wisselwerkingen tussen fotonen - Paarvorming
41-5 De golfdeeltje-dualiteit - Het principe van complementaire voorstellingen
41-6 Het golfkarakter van materie

Hoofdstuk 42 - Quantummechanica
Inleiding
42-1 Quantummechanica: een nieuwe theorie
42-2 De golffunctie en haar interpretatie - Het dubbelspleetexperiment
42-3 De onbepaaldheidsrelatie van Heisenberg
42-4 De filosofische implicaties: waarschijnlijkheid versus determinisme
42-5 De tijdonafhankelijke vorm van de Schrödingervergelijking
42-7 Vrije deeltjes - Vlakke golven en golfpakketjes
42-8 Een deeltje in een potentiaalput
42-9 Tunnelen door een barrière
Samenvatting

Hoofdstuk 43 - De quantummechanica van atomen
Inleiding
43-1 Het atoom volgens de quantummechanica
43-2 Het waterstofatoom: de vergelijking van Schrödinger en quantumgetallen

Hoofdstuk 40 - De speciale relativiteitstheorie

Inleiding
Aan het eind van de negentiende eeuw kon de natuurkunde terugzien op een periode van grote vooruitgang. De theorieën die gedurende de drie voorafgaande eeuwen waren ontwikkeld, konden op succesvolle wijze een enorme verscheidenheid van natuurlijke verschijnselen verklaren. De mechanica van Newton gaf een prachtige verklaring voor de beweging van voorwerpen op aarde en voor de beweging van hemellichamen, en had bovendien de grondslag gelegd voor succesvolle theorieën met betrekking tot vloeistofbeweging, golfbeweging en geluid. Het gedrag van gassen en andere materialen werd door de kinetische theorie verklaard. Maxwells theorie van het elektromagnetisme bood niet alleen een verklaring voor elektrische en magnetische verschijnselen (die nauw met elkaar samen bleken te hangen), maar voorspelde ook het bestaan van elektromagnetische golven die zich volgens de theorie precies zo zouden moeten gedragen als licht en zo ontstond het inzicht dat licht uit elektromagnetische golven bestaat. Het leek dan ook alsof de natuurlijke wereld, zoals gezien door de ogen van natuurkundigen, zeer goed werd begrepen. Er waren nog een paar lastige vragen over, maar men had goede hoop dat deze kwesties op basis van de bestaande theorieën spoedig zouden worden opgehelderd.
Het bleek echter anders uit te pakken. De lastige vragen die nog over waren, kwamen pas tot een oplossing toen in het begin van de twintigste eeuw twee revolutionaire nieuwe theorieën werden geformuleerd die ons hele inzicht in de natuur diepgaand hebben veranderd: de relativiteitstheorie en de quantumtheorie.
De natuurkunde zoals men die aan het eind van de negentiende eeuw kende, wordt de klassieke natuurkunde genoemd. De nieuwe natuurkunde die zich uit de grote omwentelingen aan het begin van de twintigste eeuw ontwikkelde, wordt tegenwoordig de moderne natuurkunde genoemd. In dit hoofdstuk bespreken we de speciale relativiteitstheorie, die in 1905 door Albert Einstein (1879-1955) werd geformuleerd en in het hoofdstuk dat hierop volgt, geven we een inleiding tot de al even belangrijke quantumtheorie.
terug naar de Inhoud

40-1 Relativiteit volgens Galileï en Newton
De speciale relativiteitstheorie van Einstein gaat over de manier waarop we gebeurtenissen waarnemen, met name over de manier waarop voorwerpen en gebeurtenissen worden waargenomen vanuit verschillende referentiestelsels (een groep van samenhangende voorwerpen en toestanden, een 'wereld'; bijvoorbeeld een 'trein' t.o.v. een 'station'). Dit onderwerp was natuurlijk al veel eerder bestudeerd door Galileï en Newton, en daarom beginnen we met een korte bespreking van deze oudere inzichten.
We zullen het hier in hoofdzaak hebben over zogenaamde inertiale referentiestelsels. Een inertiaal (niet veranderend, in rust verkerend) referentiestelsel (een samenhangend geheel) is een stelsel waarin de eerste wet van Newton, de traagheidswet geldt. Dat wil zeggen: als er op een voorwerp geen nettokracht wordt uitgeoefend door andere lichamen, blijft dat voorwerp in rust of blijft het met een constante snelheid langs een rechte lijn bewegen. Referentiestelsels die roteren of een andere vorm van versnelling ondergaan zijn niet inertiaal, en met zulke stelsels zullen we ons hier niet bezighouden. De aarde roteert, en is dus strikt genomen niet inertiaal, maar de afwijking is gering en daarom mogen we de aarde in de meeste gevallen wel als een inertiaalstelsel opvatten.
Een referentiestelsel dat zich met een constante snelheid verplaatst ten opzichte van een inertiaalstelsel, is ook zelf een inertiaalstelsel (bijvoorbeeld een 'vliegtuig' t.o.v. de 'aarde' of een 'trein' t.o.v. het 'perron').

Galileï en Newton waren beiden doordrongen van het inzicht dat tegenwoordig het relativiteitsprincipe wordt genoemd: de fundamentele wetten van de natuurkunde moeten in elk inertiaalstelsel dezelfde zijn. De juistheid van dit principe wordt bevestigd door allerlei verschijnselen uit het dagelijkse leven: zo bewegen voorwerpen op de vaste grond zich op dezelfde manier als in een voertuig (trein, vliegtuig) dat zich met een constante snelheid verplaatst; waarbij we aannemen dat het voertuig niet trilt of schommelt want in dat geval is het stelsel niet meer inertiaal. Wanneer u als passagier in een dergelijk voertuig een stukje wandelt, tafeltennis speelt of een muntje op de grond laat vallen, bewegen de betreffende voorwerpen precies zoals op de vaste grond.
Stel u zit in een auto die zich met een grote constante snelheid verplaatst en houdt in die auto een muntje omhoog, dat u vervolgens loslaat (a). Hoe gaat het muntje dan vallen? Het muntje valt langs een rechte lijn omlaag en treft de vloer op een plaats die loodrecht onder het punt ligt, waarin het muntje werd losgelaten. Laat u het voorwerp uit een raampje van de auto vallen, dan gebeurt dat niet, want in dat geval wordt het door de luchtstroom naar achteren geblazen. Op de vaste grond vallen voorwerpen op dezelfde manier recht omlaag (b) en de uitkomst van ons experiment in de rijdende auto klopt met het relativiteitsprincipe.

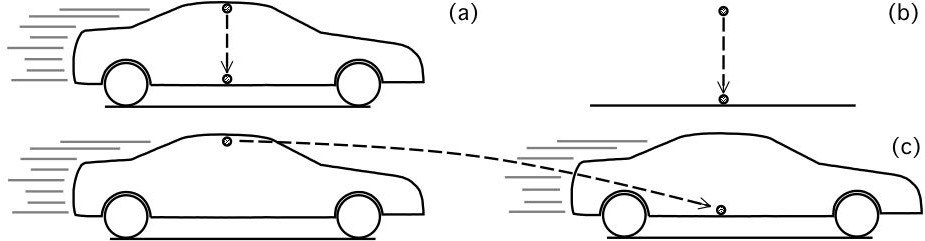Een waarnemer langs de weg ziet het voorwerp echter als een gebogen baan (paraboolbaan) volgen (c). Welke baan wordt waargenomen (loodrecht naar beneden of paraboolbaan), hangt af van het referentiestelsel waarin de waarnemer zich bevindt! Dat is echter niet in strijd met het relativiteitsprincipe, want dat zegt dat de wetten van de natuurkunde in elk inertiaalstelsel dezelfde zijn en in beide referentiestelsels geldt inderdaad dezelfde wet van de zwaartekracht, en gelden dezelfde bewegingswetten.
Het verschil tussen de beide waarnemingen is dat de munt ten opzichte van het referentiestelsel van de aarde een beginsnelheid heeft, die gelijk is aan de snelheid van de auto. De wetten van de natuurkunde voorspellen daarom dat de munt in het referentiestelsel van de aarde, net als een afgeschoten kogel, een parabolische baan zal beschrijven.
Ten opzichte van het referentiestelsel van de auto is de beginsnelheid nul en hier voorspellen de wetten van de natuurkunde dat het muntje loodrecht omlaagvalt. Kortom, de wetten zijn in beide referentiestelsels dezelfde, ook al verschillen de waargenomen banen van het muntje.
Hoe één en dezelfde gebeurtenis, beantwoordend aan dezelfde wetten, echter wordt gezien en hoe die wordt beoordeeld, is betrekkelijk, relatief: het oordeel is betrokken op het referentiestelsel waarin de waarnemer zich bevindt.

De relativiteit van Galileï en Newton gaat uit van bepaalde onbewijsbare aannamen die aansluiten bij onze alledaagse ervaring: daardoor wordt verondersteld dat bijvoorbeeld de lengte van een voorwerp en de snelheid waarmee de tijd verloopt, onafhankelijk zijn van het referentiestelsel van de waarnemer. In de klassieke mechanica worden ruimte en tijd als absoluut beschouwd: de uitkomsten van metingen van ruimte en tijd zijn onafhankelijk van het referentiestelsel. Verder wordt er aangenomen dat de massa van een voorwerp en ook de krachten niet veranderen wanneer er een ander inertiaal referentiestelsel wordt gekozen.
Het spreekt vanzelf dat de plaats en de snelheid van een voorwerp wel afhangen van het gekozen referentiestelsel. We geven een voorbeeld: stel dat iemand in een bus met een snelheid van 5 km/h naar de bestuurderscabine toeloopt. Als de bus zich met 40 km/h ten opzichte van de aarde verplaatst, heeft de wandelende passagier ten opzichte van de aarde een snelheid van 45 km/h. De versnelling van een lichaam is echter, volgens de klassieke mechanica in elk inertiaal referentiestelsel gelijk, omdat de verandering in de snelheid en de tijd onafhankelijk is van het gekozen stelsel. Stel bijvoorbeeld dat de buspassagier zijn snelheid ten opzichte van de bus in 1,0 seconden van 0 tot 5 km/h vergroot, dan ondergaat hij ten opzichte van de bus een versnelling van a = 5 km/h. Ten opzichte van de aarde is de versnelling dan (45 km/h - 40 km/h)/(1,0 s) = 5 km/h/s, en dat is dezelfde waarde.
Daar F, m, en a niet afhangen van het referentiestelsel, geldt ook de tweede wet van Newton: F = ma, onafhankelijk van het gekozen referentiestelsel. Deze wet beantwoordt dus aan het relativiteitsprincipe en er kan gemakkelijk worden aangetoond dat ook de andere wetten van de mechanica aan het relativiteitsprincipe voldoen.
Dat de wetten van de mechanica in elk referentiestelsel gelijk zijn, impliceert dat geen enkel inertiaalstelsel zich in enig opzicht van andere onderscheidt; deze belangrijke conclusie kan als volgt worden geformuleerd: alle inertiale referentiestelsels zijn equivalent waar het de beschrijving van mechanische verschijnselen betreft. Het ene inertiale referentiestelsel is niet beter dan het andere. Een referentiestelsel dat verbonden is met een auto of vliegmachine die zich verplaatst, is net zo goed als een referentiestelsel dat vast met de aarde is verbonden. Wanneer u in een auto of vliegmachine zit die zich met een constante snelheid verplaatst, mag u dus evengoed stellen dat u in rust verkeert, en dat het de aarde is die beweegt. Met geen enkel experiment is vast te stellen welk referentiestelsel 'werkelijk' in rust verkeert of beweegt en het is dus niet mogelijk een bepaald referentiestelsel aan te wijzen dat in absolute rust verkeert.

In de tweede helft van de negentiende eeuw veranderde de situatie enigszins. Toen Maxwell zijn compacte, volledige en zeer succesvolle theorie van het elektromagnetisme naar voren bracht, toonde hij aan dat licht als een elektromagnetische golf kan worden beschouwd. De vergelijkingen van Maxwell voerden tot de voorspelling dat c, de lichtsnelheid, 3,00 x 10⁸ m/s bedraagt, een theoretische voorspelling die binnen de experimenteerfout overeenkwam met de waarde die werd gemeten. Daarbij deed zich de volgende vraag voor: ten opzichte van welk referentiestelsel heeft licht de waarde uit de theorie van Maxwell? Want men ging er toen van uit dat de lichtsnelheid afhankelijk is van de snelheid van het referentiestelsel.
Als bijvoorbeeld waarnemers in een raket met een snelheid van 1,0 x 10⁸ m/s naar de lichtbron toe vliegen, zouden we verwachten dat ze voor de snelheid van licht dat op hen afkomt, een waarde meten van 3,0 x 10⁸ m/s + 1,0 x 10⁸ m/s = 4,0 x 10⁸ m/s. De vergelijkingen van Maxwell bieden echter geen mogelijkheid rekening te houden met relatieve snelheid. Ze voorspellen dat de lichtsnelheid 3,0 x 10⁸ m/s bedraagt en daaruit leek te volgen dat er een bijzonder referentiestelsel moest bestaan waarin c de waarde 3,0 x 10⁸ m/s heeft.
Golven verplaatsen zich in water en langs snaren, en geluidsgolven planten zich voort door lucht en door andere materialen. Negentiende eeuwse natuurkundigen interpreteerden de stoffelijke wereld in termen van de wetten van de mechanica en namen als vanzelfsprekend aan dat ook licht zich door een of ander medium voortplant; dit transparante medium werd de ether genoemd. Men veronderstelde dat de gehele ruimte ermee was gevuld en daarom werd er aangenomen dat de lichtsnelheid die uit de vergelijkingen van Maxwell volgde, de snelheid was ten opzichte van deze ether.
Er bleek echter dat de vergelijkingen van Maxwell niet voldeden aan het relativiteitsprincipe: de vergelijkingen waren niet in elk referentiestelsel gelijk. Ze waren het eenvoudigst in het stelsel waarin c = 3,00 x 10⁸ m/s - dat wil zeggen, in een stelsel dat ten opzichte van de ether in rust verkeert. In elk ander referentiestelsel zouden er extra termen moeten worden toegevoegd om rekening te houden met de relatieve snelheid. Terwijl dus de meeste wetten van de natuurkunde voldeden aan het relativiteitsprincipe, gold dat kennelijk niet voor de wetten van elektriciteit en magnetisme (ofwel 'elektrodynamica'). Uit deze wetten leek te volgen dat er een referentiestelsel moest bestaan dat beter was dan elk ander stelsel - een referentiestelsel dat in absolute rust verkeert.

Het duurde niet lang of natuurkundigen probeerden te meten wat de snelheid van de aarde is ten opzichte van dit absolute stelsel en daartoe werden er een aantal experimenten verzonnen. Het meest directe experiment werd uitgevoerd door A.A. Michelson en E.W. Morley. In het kort komt het erop neer dat ze verschillen probeerden te meten tussen lichtsnelheden in verschillende richtingen. Ze verwachtten verschillen te vinden die afhankelijk zouden zijn van de oriëntatie van hun apparaat ten opzichte van de ether. Welke snelheid een boot heeft ten opzichte van de grond hangt af van de vraag of de boot stroomopwaarts, stroomafwaarts of dwars op de stroom vaart, en analoog zouden we ook verwachten dat de lichtsnelheid afhangt van de snelheid die de ether heeft ten opzichte van de aarde.
Vreemd genoeg vonden ze geen enkel verschil en deze uitkomst vormde een groot raadsel. Gedurende een aantal jaren werden er diverse mogelijke verklaringen naar voren gebracht, maar al die verklaringen voerden tot contradicties of waren om andere redenen onbevredigend.
In 1905 kwam Albert Einstein met een radicaal nieuwe theorie die al deze problemen op elegante wijze tot een oplossing bracht en die diepgaande veranderingen teweegbracht in onze opvattingen over ruimte en tijd.
terug naar de Inhoud

40-3 Postulaten van de speciale relativiteitstheorie
De problemen betreffende de theorie van het elektromagnetisme en de mechanica van Newton, waarop men tegen het einde van de negentiende eeuw was gestuit, werden op schitterende wijze opgelost toen Einstein in 1905 zijn speciale relativiteitstheorie naar voren bracht. Naar het schijnt werd Einstein daarbij niet direct beïnvloed door het nulresultaat van het experiment van Michelson Morley. Hij had met bewondering het theoretische werk van Lorentz bestudeerd. Wat Einstein dreef waren bepaalde vragen die betrekking hadden op de theorie van het elektromagnetisme en op lichtgolven. Hij vroeg zich bijvoorbeeld af: "Wat zou ik zien als ik meereed op een lichtstraal?" Het antwoord was dat hij dan geen voortgaande elektromagnetische golf zou zien, maar elektrische en magnetische velden in rust, waarvan de sterkte van punt tot punt verschilt, maar niet in de tijd verandert. Zulke velden, zo realiseerde Einstein zich, waren nooit waargenomen en waren in feite in strijd met de elektromagnetische theorie van Maxwell. Daarom betoogde hij dat het onredelijk was te denken dat de snelheid van licht ten opzichte van een waarnemer ooit nul kon zijn, of meer algemeen, ooit kleiner kon zijn dan c, en dit laatste werd het tweede postulaat van zijn relativiteitstheorie.
Einstein trok de conclusie dat de inconsistenties die hij aantrof in de theorie van het elektromagnetisme een gevolg waren van de aanname dat er een absolute ruimte bestaat. In zijn beroemde artikel van 1905 kwam hij met het voorstel het idee van de ether volledig te verlaten en daarmee ook af te zien van de aanname dat er een absoluut referentiestelsel bestaat dat in rust verkeert. Dit voorstel gaf hij de vorm van twee postulaten. Het eerste postulaat vervangt het relativiteitsprincipe van Newton door een algemener relativiteitsprincipe, dat niet alleen betrekking heeft op de mechanica, maar ook op de rest van de natuurkunde, elektriciteit en magnetisme inbegrepen:

Eerste postulaat (het relativiteitsprincipe):
De wetten van de natuurkunde hebben in elk inertiaalstelsel dezelfde vorm.
Tweede postulaat (de onveranderlijkheid van de lichtsnelheid): Licht plant zich door lege ruimte voort met een vaste snelheid c, die onafhankelijk is van de snelheid van de bron of de waarnemer.
Deze twee postulaten vormen de grondslag van de speciale relativiteitstheorie van Einstein. Het voorvoegsel 'speciale' geeft het onderscheid aan met Einsteins latere 'algemene relativiteitstheorie', die over niet-inertiaalstelsels gaat, dus over referentiestelsels die versnelling ondergaan. De speciale theorie heeft alleen betrekking op inertiaalstelsels, stelsels die in rust zijn.

Het tweede postulaat lijkt het moeilijkst te aanvaarden, want het is in meerdere opzichten in strijd met het 'gezonde verstand'. Ten eerste moeten we ons nu voorstellen dat licht zich voortplant door lege ruimte. Het is echter niet al te moeilijk afstand te doen van de ether, want niemand is er ooit in geslaagd de ether aan te tonen. Het tweede postulaat zegt ons echter ook dat de lichtsnelheid in vacuüm altijd dezelfde is, c = 3,00 x 10⁸ m/s, ongeacht de snelheid van de waarnemer of de bron. Iemand die zich naar een bron toe of van een bron af beweegt, meet dus dezelfde lichtsnelheid als iemand die ten opzichte van de bron in rust verkeert; en dit is strijdig met onze alledaagse ervaring, want we zouden verwachten dat de snelheid van de waarnemer bij de snelheid van het licht moet worden opgeteld.
Deel van de moeilijkheid is dat de snelheden waarmee we in ons dagelijkse leven te maken hebben, altijd veel kleiner zijn dan de lichtsnelheid. We mogen er in feite niet zo maar van uitgaan dat onze gewone ervaring ook van toepassing is waar het gaat om een zo extreem hoge snelheid. Bovendien stemt het tweede postulaat volledig overeen met het nulresultaat van het experiment van Michelson Morley.
De elegantie van het voorstel van Einstein is duidelijk. Want door het idee van een absoluut referentiestelsel los te laten, werd het mogelijk Maxwells theorie van het elektromagnetisme te verzoenen met de mechanica. De lichtsnelheid die door de vergelijkingen van Maxwell wordt voorspeld, is de lichtsnelheid in vacuüm in elk willekeurig referentiestelsel.
De theorie van Einstein vereist dat we onze beperktheid voor wat betreft onze voorstellingen van ruimte en tijd beseffen. In de nu volgende paragrafen bekijken we een aantal vreemde, maar interessante consequenties van de speciale relativiteitstheorie. De redeneringen die we daarbij volgen zijn meestal eenvoudig. We zullen gebruik maken van een methode die ook door Einstein zelf werd toegepast: we stellen ons heel eenvoudige experimentele situaties voor waarin weinig wiskunde nodig is. Op deze manier kunnen we de consequenties van de relativiteitstheorie begrijpen zonder ons in ingewikkelde berekeningen te begeven. Einstein sprak in dit verband van 'gedachtenexperimenten'. De wiskundige aspecten worden later behandeld.
terug naar de Inhoud

40-4 Gelijktijdigheid
Een van de belangrijke consequenties van de relativiteitstheorie is dat tijd niet langer als een absolute grootheid mag worden opgevat. Tijd stroomt voort, zonder ooit om te keren en daaraan wordt door de relativiteitstheorie niets veranderd. Maar het tijdsinterval tussen twee gebeurtenissen en ook de vraag of twee gebeurtenissen zich gelijktijdig voordoen, hangt af van het referentiestelsel waarin de waarnemer zich bevindt.
Van twee gebeurtenissen zeggen we dat ze gelijktijdig zijn, als ze op hetzelfde tijdstip plaatsvinden. Maar hoe kunnen we dat vaststellen? Wanneer de gebeurtenissen in hetzelfde punt in de ruimte plaatsvinden, bijvoorbeeld wanneer twee appels precies tegelijkertijd op uw hoofd vallen, is er geen probleem. Maar als de twee gebeurtenissen zich voordoen in punten die ver uiteenliggen, is het moeilijker uit te maken, want in dat geval moeten we rekening houden met de tijd die het licht erover doet ons te bereiken. Doordat licht zich met een eindig grote snelheid voortplant, moet de waarnemer de twee gebeurtenissen in dit laatste geval terugrekenen om na te gaan wanneer die gebeurtenissen werkelijk hebben plaatsgevonden. Als bijvoorbeeld twee gebeurtenissen op hetzelfde moment worden waargenomen, terwijl de ene gebeurtenis in feite verder van de waarnemer plaatsvond dan de andere, moet de eerstgenoemde gebeurtenis zich het eerst hebben voorgedaan en waren de twee gebeurtenissen dus niet gelijktijdig.

We maken nu geen berekeningen, maar doen we een gedachtenexperiment. We nemen aan dat een waarnemer, O (observator) genaamd, zich halverwege de punten A en B bevindt waar de twee gebeurtenissen plaatsvinden. We kunnen ons bijvoorbeeld voorstellen dat A en B door de bliksem worden getroffen. Wanneer het om een korte gebeurtenis gaat zoals een blikseminslag, vertrekken vanuit A en B slechts korte lichtpulsen naar O. De waarnemer ziet de gebeurtenissen op het tijdstip dat de lichtpulsen hem bereiken. Als de twee pulsen gelijktijdig bij O aankomen, moeten ook de twee oorspronkelijke gebeurtenissen gelijktijdig hebben plaatsgevonden. De twee lichtflitsen hebben immers dezelfde voortplantingssnelheid en daar de afstanden OA en OB gelijk zijn, doet het licht er even lang over om van A naar O te gaan, als van B naar O.
De waarnemer O kan in dit geval met zekerheid stellen dat de twee gebeurtenissen gelijktijdig hebben plaatsgevonden. Als O het licht van de ene gebeurtenis daarentegen eerder ziet dan het licht van de andere gebeurtenis, is het zeker dat de eerstgenoemde gebeurtenis het eerst optrad.

De vraag waar het ons vervolgens om gaat, is: als een waarnemer in een referentiestelsel twee gebeurtenissen als gelijktijdig ziet, zijn ze dan ook gelijktijdig voor een andere waarnemer in een ander referentiestelsel, dat zich ten opzichte van de eerste waarnemer verplaatst? We noemen nu de waarnemers O₁ en O₂ en nemen aan dat ze elk op een vaste plaats in respectievelijk de referentiestelsels 1 en 2 zitten, die ten opzichte van elkaar een snelheid v hebben. We stellen ons deze twee referentiestelsels voor als twee treinen naast elkaar. O₂ zegt dat O₁ met een snelheid v naar rechts beweegt, zoals in (a); O₁ zegt dat O₂ naar links beweegt, zoals in (b). Volgens het relativiteitsprincipe zijn beide gezichtspunten correct. Er bestaat geen derde gezichtspunt dat ons vertelt welke waarnemer zich 'werkelijk' verplaatst.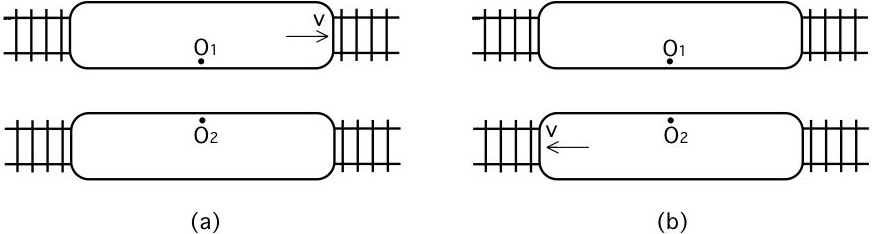

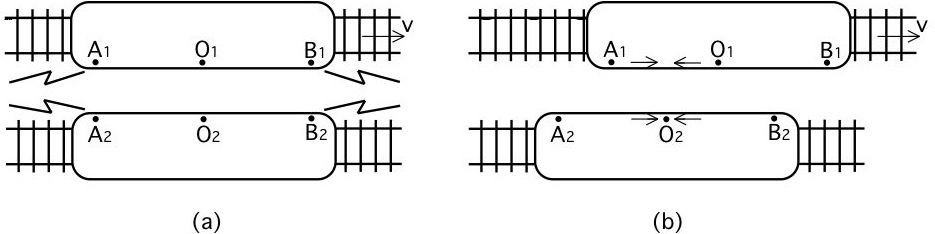
Stel nu dat er twee gebeurtenissen plaatsvinden die door beide waarnemers worden gezien. We nemen weer aan dat de twee gebeurtenissen een blikseminslag betreffen en dat beide bliksemstralen op de plaats waar ze inslaan een merkteken op beide treinen achterlaten: de inslagpunten op de trein van O₁ zijn A₁ en B₁, en de inslagpunten op de trein van O₂ zijn A₂ en B₂. We nemen aan dat O₁ zich halverwege A₁ en B₁ bevindt en dat O₂ zich halverwege A₂ en B₂ bevindt.
Laten we vervolgens aannemen dat we in het referentiestelsel van O₂ zijn, zodat we O₁ met een snelheid v naar rechts zien bewegen. Bovendien nemen we aan dat de twee gebeurtenissen in het referentiestelsel van O₁ en O₂ gelijktijdig plaatsvinden en wel op het tijdstip waarop O₁ en O₂ zich tegenover elkaar bevinden (a). Een korte tijdsduur later (b) bereikt het licht vanuit A₂ en B₂ gelijktijdig de waarnemer O₂. Doordat O₂ door meting heeft vastgesteld dat de afstanden O₂-A₂ en O₂-B₂ gelijk zijn, weet O₂ dat de twee gebeurtenissen gelijktijdig hebben plaatsgevonden.
Maar wat ziet van ons uit gezien waarnemer O₁? Vanuit ons referentiestelsel (het stelsel van O₂) kunnen we zien dat O₁ zich naar rechts verplaatst gedurende de tijd waarin het licht vanuit A₁ en B₁ naar O₁ gaat. Zoals figuur (b) laat zien, is van ons uit gezien het licht van B₁ waarnemer O₁ al gepasseerd, terwijl het licht dat van A₁ komt O₁ nog niet heeft bereikt. Het is dus duidelijk dat van ons uit gezien O₁ het licht dat van B₁ komt, eerder moet hebben gezien dan het licht dat van A₁ komt.
Het referentiestelsel van O₁ is net zo goed als dat van O₂. De lichtsnelheid is voor O₁ even groot als voor O₂ en is over het traject van A₁ naar O₁ even groot als over het traject van B₁ naar O₁. Daar de afstand O₁-A₁ gelijk is aan O₁-B₁, moet waarnemer O₂ tot de conclusie komen dat voor waarnemer O₁ de gebeurtenis in B₁ eerder plaatsvond dan de gebeurtenis in A₁.

We vinden dus dat twee gebeurtenissen die, zoals gezien door de ene waarnemer, gelijktijdig plaatsvinden, van die ene waarnemer uit gezien niet als gelijktijdig worden gezien door een tweede waarnemer. De waarnemer uit het ene referentiestelsel stelt voor de andere waarnemer iets anders vast, dan de andere waarnemer zelf waarneemt. Die stelt voor zichzelf namelijk wel gelijktijdigheid vast.
Volgens het relativiteitsprincipe kan de redenering die we in ons gedachtenexperiment hebben ontwikkeld, net zo goed worden opgezet vanuit het referentiestelsel van O₁. In dat geval verkeert waarnemer O₁ in rust, en ziet hij gebeurtenis B₂ voordat hij gebeurtenis A₂ ziet. Maar O₁ zal onderkennen dat O₂ die zich dan met een snelheid v naar links verplaatst, de twee gebeurtenissen wel als gelijktijdig ziet. In het dagelijkse leven bestaat dit verschil in waarneming wel, maar merken we daar niets van; het effect wordt pas van betekenis wanneer de twee referentiestelsels ten opzichte van elkaar een zeer grote snelheid hebben (in de buurt van c) of wanneer het om zeer grote afstanden gaat.
De vraag kan worden gesteld: "Welke waarnemer heeft gelijk, O₁ of O₂?" Volgens het relativiteitsprincipe is het antwoord dat beiden gelijk hebben. Er bestaat geen 'beste' referentiestelsel op grond waarvan we kunnen uitmaken welke waarnemer gelijk heeft. Beide stelsels zijn even goed. De conclusie is dat gelijktijdigheid geen absoluut begrip is, maar relatief.
terug naar de Inhoud

40-5 Tijddilatatie en de tweelingparadox
Het feit dat twee gebeurtenissen die door de ene waarnemer als gelijktijdig worden gezien, niet noodzakelijk gelijktijdig zijn in de ogen van een andere waarnemer, geeft aan dat tijd zelf niet absoluut is. Is het mogelijk dat de tijd in het ene referentiestelsel langzamer of sneller voorbijgaat dan in het andere? Dat is inderdaad wat de relativiteitstheorie van Einstein voorspelt. We laten zien waarom door opnieuw een gedachtenexperiment uit te voeren.
De tekening toont een ruimteschip dat met grote snelheid de aarde passeert. Tekening (a) laat zien wat een bemanningslid van het ruimteschip waarneemt en (b) is getekend vanuit het gezichtspunt van een waarnemer op aarde. Beide waarnemers bezitten een nauwkeurige klok. De man in het ruimteschip (a) merkt niets van de eigen snelheid. Hij laat vanuit een lichtbron een lichtbundel vertrekken met lichtsnelheid c en meet de tijd die het licht erover doet om van de bron naar de spiegel en weer terug te reizen. Het tijdsinterval van het inertiaal referentiestelsel dat voor de waarnemer stilstaat, wordt de eigentijd genoemd.

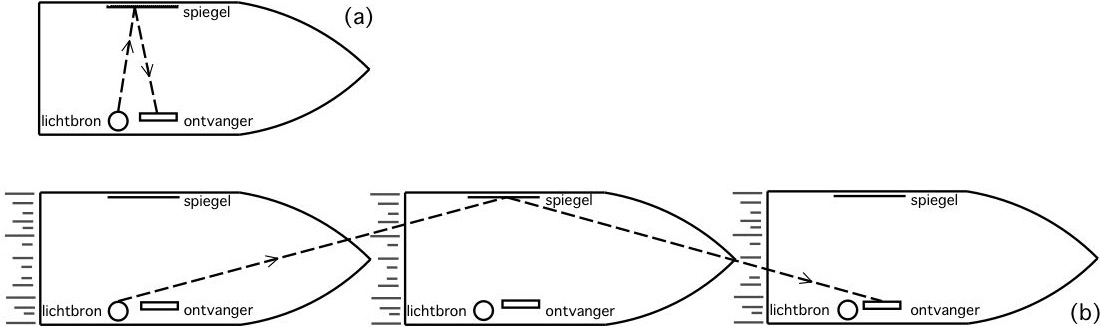De gebeurtenissen in het ruimteschip worden ook gevolgd door de waarnemer op aarde, maar in de ogen van deze waarnemer is het ruimteschip in beweging (b). Terwijl het licht in het ruimteschip van de bron naar de spiegel gaat en vandaar naar de ontvanger, legt het licht de twee schuine trajecten af die in (b) zijn getekend. Ook voor de waarnemer op aarde is de lichtsnelheid gelijk aan c, maar deze waarnemer ziet het licht een grotere afstand afleggen. Wanneer beide waarnemers meten hoe lang het licht erover doet in het ruimteschip van bron naar ontvanger te gaan, vindt de waarnemer op aarde een langere tijdsduur dan de waarnemer aan boord van het ruimteschip.
De tijdsduur tussen de twee gebeurtenissen (het uitzenden van het licht en de aankomst bij de ontvanger) is voor de waarnemer op aarde groter dan voor de waarnemer in het ruimteschip. Dit is een algemeen geldig resultaat van de relativiteitstheorie en het effect staat bekend als tijddilatatie (tijdsuitzetting, tijdsverlenging). Eenvoudig geformuleerd komt tijddilatatie neer op het volgende: bewegende klokken blijken langzamer te lopen, de tijd wordt uitgerekt. Er is niets mis met de klokken, zij werken goed. De conclusie is dat in een referentiestelsel dat zich ten opzichte van ons verplaatst, wij tijd langzamer zien verlopen!

Het idee van tijddilatatie is moeilijk te accepteren, want het botst met ons gezonde verstand. Berekeningen laten zien dat tijddilatatie bij gewone snelheden een verwaarloosbaar klein effect heeft; zij is alleen van betekenis wanneer v niet heel veel kleiner is dan c. De snelheden die we in het dagelijkse leven tegenkomen, zijn altijd zeer veel kleiner dan c en daardoor merken we gewoonlijk niets van tijddilatatie.
Er zijn experimenten gedaan om het effect van tijddilatatie te meten en de uitkomst van die metingen stemt overeen met de voorspellingen van Einstein. Zo werden er in 1971 uiterst nauwkeurige atoomklokken in vliegtuigen de wereld rondgevlogen. Daar de snelheid van vliegtuigen (1000 km/h) veel kleiner is dan c, was de te verwachten tijddilatatie zo gering, dat men voor detectie klokken nodig had die tot op nanoseconden (10^-9 s) nauwkeurig waren. De uitkomst van het experiment bleek binnen de experimenteerfout overeen te stemmen met de berekeningen.
De realiteit van tijddilatatie was overigens al tientallen jaren eerder bevestigd door waarnemingen aan 'elementaire deeltjes'. Doordat zulke deeltjes een zeer kleine massa hebben (gewoonlijk 10^-27 tot 10^-30 kg), kost het weinig energie ze te versnellen tot snelheden in de buurt van c. Veel van deze elementaire deeltjes zijn instabiel en vallen na verloop van tijd in eenvoudiger deeltjes uiteen. Een voorbeeld van zo'n instabiel deeltje is het muon, dat in rust een gemiddelde levensduur heeft van 2,2 ps. Nauwkeurige experimenten hebben aangetoond dat het muon een grotere levensduur heeft wanneer het zich met hoge snelheid verplaatst en de waargenomen toename in levensduur stemt overeen met wat door de formule voor tijddilatatie wordt voorspeld.

Het fenomeen tijddilatatie was aanleiding tot een interessante speculatie aangaande het reizen in de ruimte. Toen we nog niets van tijddilatatie wisten, leek het principieel onmogelijk dat gewone stervelingen ooit een ster zouden kunnen bereiken die 100 lichtjaar van ons afstaat (1 lichtjaar is de afstand die licht in 1 jaar kan afleggen, en komt dus overeen met 3,0 x 10⁸ m/s x 3,15 x 10⁸ s = 9,5 x 10⁸ m). Want zelfs als een ruimteschip met bijna de lichtsnelheid zou reizen, zou het nog altijd meer dan 100 jaar duren voordat de ster werd bereikt. Maar de wiskundige formule waarmee tijddilatatie kan worden berekend, zegt ons dat voor een astronaut de reisduur korter zou zijn. In een ruimteschip dat zich met een snelheid v = 0,999c verplaatst, zou de reis niet langer dan ongeveer 4,5 jr duren. Dankzij de tijddilatatie zou een mens zo'n reis dus in principe kunnen maken. Het lijkt echter uitgesloten dat het enorme probleem om zulke hoge snelheden te realiseren binnen afzienbare tijd zal worden opgelost.
Merk in dit voorbeeld op dat er op aarde 100 jaar zouden verstrijken, terwijl de reis voor de astronaut maar 4,5 jaar zou duren. Zijn het alleen de klokken in het ruimtevoertuig die langzamer lopen? Het antwoord luidt nee. Alle processen, inclusief levensprocessen, verlopen voor de astronaut (zoals gezien door waarnemers op aarde) langzamer. Maar de astronaut zou zelf niets bijzonders ervaren: voor hem zou de tijd op een normale manier voorbijgaan en hij zou dus 4,5 jaar lang op een normale manier slapen, eten, lezen, enzovoort. Tegelijk zouden mensen op aarde 100 jaar lang op de gewone manier leven.

Niet lang nadat Einstein de speciale relativiteitstheorie had gepubliceerd, werd er een schijnbare paradox gevonden, de zogenaamde 'tweelingparadox'. Stel dat een 20 jarige tweeling met zeer hoge snelheid naar een verre ster afreist, daar omkeert en weer terugreist, terwijl de andere tweeling achterblijft op aarde. Volgens de tweeling die op aarde blijft, zal de reizende tweeling minder verouderen dan hijzelf: terwijl er voor de aardse tweeling 20 jaar voorbijgaan, gaat er voor de reizende tweeling misschien maar 1 jaar voorbij (afhankelijk van de snelheid van het ruimtevaartuig). Wanneer de reiziger tenslotte terugkeert, zal de tweeling die op aarde is gebleven 40 jaar oud zijn, terwijl zijn reizende broer dan nog maar 21 is. Dit alles is het gezichtspunt van de tweeling op aarde.
Maar hoe zit het met de reizende tweeling? Als alle inertiaalstelsels gelijkwaardig zijn, zal de reizende tweeling dan niet precies hetzelfde beweren als de tweeling op aarde, maar dan omgekeerd? Kan de tweeling die astronaut is niet evengoed stellen dat de aarde zich met hoge snelheid van het ruimtevaartuig verwijdert, en dat de tijd op aarde dus langzamer verloopt, zodat de tweeling op aarde minder veroudert? Dit is het tegenovergestelde van wat de tweeling op aarde voorspelt. Ze kunnen niet allebei gelijk hebben, want uiteindelijk keert het ruimtevaartuig op aarde terug, en dan kunnen de leeftijden en de klokken direct met elkaar worden vergeleken.
Toch is dit geen paradox. De implicaties van de speciale relativiteitstheorie - in dit geval het verschijnsel tijddilatatie - gelden alleen voor waarnemers in inertiaalstelsels. De aarde is zo'n stelsel (althans in goede benadering), maar het ruimtevaartuig niet, want het ruimtevaartuig ondergaat aan het begin en aan het einde van zijn reis een versnelling en wat nog belangrijker is, het ruimtevaartuig ondergaat eveneens een versnelling wanneer dat - in het verste punt aangekomen - van richting omkeert. Gedurende deze perioden van versnelling zijn de voorspellingen van de astronaut, gebaseerd op de speciale relativiteitstheorie, niet geldig. De tweeling op aarde bevindt zich in een inertiaalstelsel en kan wel geldige voorspellingen doen. Er is dus geen sprake van een paradox. Het gezichtspunt van de reizende tweeling is niet correct. De voorspellingen van de tweeling op aarde zijn echter wel geldig en de voorspelling dat de reizende tweeling bij zijn terugkeer minder is verouderd dan de achterblijver, is de juiste.
terug naar de Inhoud

40-6 Lengtecontractie
Volgens de speciale relativiteitstheorie hangen niet alleen tijdsintervallen, maar ook ruimte-intervallen: lengten en afstanden, af van het referentiestelsel waarin de waarnemer zich bevindt. In de tekening toont (a) de toestand voor de waarnemer in een ruimtevaartuig. Vanuit het referentiestelsel van de astronaut gezien, verkeert het ruimteschip in rust en verplaatsen de Aarde en Neptunus zich met de hoge snelheid v.
Een waarnemer op aarde (b) ziet het ruimtevaartuig met de hoge snelheid v van de Aarde naar Neptunus vliegen. De afstand tussen beide planeten, zoals gemeten door deze waarnemer, bedraagt L. Gemeten vanaf de aarde is de tijd die de reis duurt de afstand L gedeeld door de snelheid v: t = L/v (want in het algemeen geldt dat de snelheid (v) gelijk is aan de afgelegde weg (s) per tijdseenheid (t): v = s/t en t = s/v).
Maar door de tijddilatatie bij hoge snelheid is de duur van de reis, dus de tijd tussen het vertrek van de aarde en de aankomst op Neptunus, langer voor de waarnemer die de reis vanaf de aarde observeert dan voor de astronaut in het ruimteschip, voor wie de duur en daardoor ook de afstand korter is (a).
De waarnemer die het ruimteschip vanaf de aarde volgt, meet dezelfde snelheid, maar meet een langer tijdsinterval tussen vertrek en aankomst en dat betekent (door de formule t = L/v) dat niet alleen de tijd, maar ook de afstand die hij meet langer moet zijn (b).

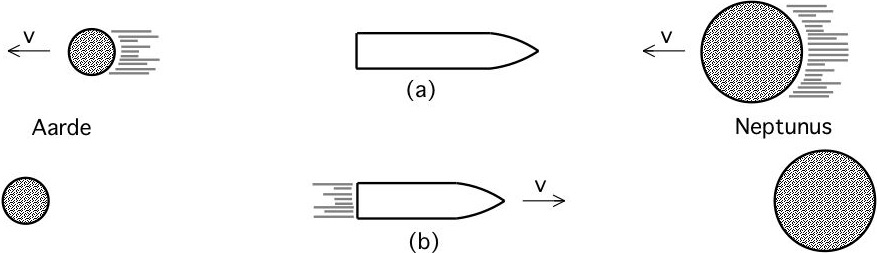Dit is een algemeen geldige uitkomst van de speciale relativiteitstheorie, die zowel voor de lengte van voorwerpen als voor afstanden geldt. Dit kan het eenvoudigst als volgt worden geformuleerd: wanneer een voorwerp zich verplaatst, wordt er voor dat voorwerp (vanuit een ander referentiestelsel) een kleinere lengte gemeten dan wanneer het in rust verkeert. Dit effect noemt men lengtecontractie.
De lengte L in de vergelijking t = L/v wordt de eigenlengte genoemd. De eigenlengte van een voorwerp (of van de afstand tussen twee punten) is de lengte die wordt gemeten door een waarnemer die ten opzichte van het voorwerp (of de twee punten) in rust verkeert.
Men dient in het oog te houden dat de lengtecontractie zich alleen voordoet langs de bewegingsrichting. Zo wordt de lengte van het voortreizende ruimteschip in de tekening verkort, maar de diameter is gelijk aan de diameter die het ruimteschip heeft wanneer het in rust verkeert. In het dagelijkse leven is lengtecontractie net zo min waar te nemen als tijddilatatie; dit doet zich voornamelijk voor als de snelheid v zeer groot is.
terug naar de Inhoud

40-7 Vierdimensionale ruimte-tijd
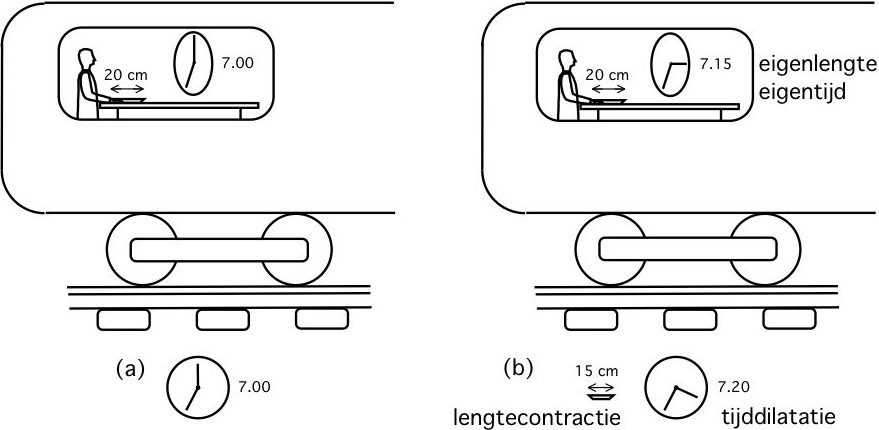
Stel een reiziger zit in een trein die zich verplaatst met een extreem hoge snelheid van bijvoorbeeld 0,65c. Volgens een klok in de trein is het op het moment dat de reiziger aan zijn maaltijd begint 7.00 uur en is het 7.15 uur wanneer hij ermee klaar is. Beide gebeurtenissen, begin en einde van de maaltijd, vinden plaats op dezelfde plek in de trein en de eigentijd tussen deze twee gebeurtenissen bedraagt 15 min.
Voor waarnemers op de grond duurt de maaltijd van onze reiziger langer, n.l. 20 min. volgens de wiskundige berekening. Laten we aannemen dat de maaltijd werd opgediend op een bord met een diameter van 20 cm. Voor waarnemers op de grond is dit bord maar 15 cm breed (lengtecontractie). Voor waarnemers op de grond lijkt de hoeveelheid voedsel kleiner, maar wordt er langer over het eten gedaan.

De relativistische effecten tijddilatatie en lengtecontractie houden elkaar in zeker opzicht in evenwicht. Gezien vanaf de grond krijgt het voedsel wat het in omvang verliest er aan duurzaamheid bij. Ruimte, ofwel lengte wordt uitgewisseld tegen tijd.
Dit soort overwegingen voerden tot de aanname van een vierdimensionale ruimte-tijd: ruimte heeft drie dimensies en tijd is een vierde dimensie. Ruimte en tijd hangen nauw met elkaar samen. Wanneer een ballon wordt samengedrukt, wordt de omvang kleiner en de druk groter, en iets overeenkomstigs gebeurt wanneer voorwerpen en gebeurtenissen worden bekeken vanuit een ander referentiestelsel: een bepaalde hoeveelheid ruimte wordt uitgewisseld tegen tijd, of omgekeerd.

Het idee van vier dimensies komt u wellicht wat vreemd voor, maar het wil eigenlijk zeggen dat een gebeurtenis wordt gespecificeerd door vier grootheden: drie grootheden die de plaats in de ruimte beschrijven en een grootheid die aangeeft op welk moment in de tijd de gebeurtenis plaatsvond. Dit alles is niets bijzonders, maar wat echt ongewoon is aan vierdimensionale ruimte-tijd, is dat ruimte en tijd uitwisselbaar zijn: wanneer er van referentiestelsel wordt veranderd, kan een beetje van het ene worden uitgewisseld tegen een beetje van het andere.
Voor de meesten van ons is vierdimensionale ruimte-tijd een moeilijk begrip. Op de een of andere manier hebben we, net als de natuurkundigen uit periode vóór de relativiteitstheorie, het gevoel dat ruimte en tijd twee volkomen verschillende zaken zijn, en toch geven onze gedachtenexperimenten aan dat ruimte en tijd niet volkomen los staan van elkaar. De moeite die het ons kost dit te accepteren, doet denken aan de situatie die in de zeventiende eeuw in de tijd van Galileï en Newton bestond. Voor de tijd van Galileï hield men de verticale richting - de bewegingsrichting van vallende voorwerpen - voor een dimensie die volkomen anders was dan de twee horizontale dimensies. Galileï liet zien dat de verticale dimensie alleen maar de richting is waarin de zwaartekracht toevallig werkt. Voor het overige zijn de drie dimensies volkomen equivalent, een feit dat iedereen tegenwoordig accepteert. Nu wordt van ons gevraagd nog een dimensie meer te accepteren, namelijk tijd, een grootheid die voorheen werd opgevat als iets van totaal andere aard dan de drie ruimtelijke dimensies.
We willen hiermee niet beweren dat tijd en ruimte zich in geen enkel opzicht van elkaar onderscheiden: wat de relativiteitstheorie heeft aangetoond, is dat ruimte- en tijdbepalingen niet onafhankelijk zijn van elkaar.
terug naar de Inhoud

40-9 Relativistische massa en impuls
De drie fundamentele grootheden van de mechanica zijn lengte, tijd en massa. De eerste twee grootheden zijn, zoals we hebben laten zien, relatief - want de waarde van die grootheden hangt af van het referentiestelsel waarin ze worden gemeten - en het ligt daarom voor de hand dat ook massa een relatieve grootheid is. Inderdaad blijkt de massa van een voorwerp groter te worden naarmate de snelheid van dat voorwerp toeneemt. Dit is de relativistische massa.
terug naar de Inhoud

40-10 De hoogst mogelijke snelheid
Een fundamentele consequentie van de speciale relativiteitstheorie is dat de snelheid van een voorwerp nooit gelijk aan of groter kan worden dan de lichtsnelheid. De lichtsnelheid vormt een natuurlijke grens voor snelheden in het heelal. Naarmate een voorwerp meer en meer wordt versneld, wordt de impuls van dat voorwerp steeds groter. Zou v gelijk worden aan c, dan wordt de noemer van de vergelijking nul en wordt de impuls oneindig groot. Het vraagt daarom een oneindige hoeveelheid energie een voorwerp te versnellen tot een snelheid v = c en zoiets is onmogelijk.
Als v groter was dan c, zou de uitkomst van de wiskundige formule voor de relativiteit de wortel uit een negatief getal zijn; de waarden van lengten, tijdsintervallen en massa zouden in dat geval dus imaginair zijn, en daarom concluderen we dat de snelheid van gewone voorwerpen niet groter kan zijn dan de lichtsnelheid. Tegen het einde van de jaren zestig werd echter aangetoond dat de vergelijkingen van Einstein niet uitsluiten dat er voorwerpen bestaan waarvan de snelheid altijd groter is dan c. Als zulke deeltjes bestaan (men heeft deze hypothetische deeltjes 'tachyonen' gedoopt, 'tachyon' betekent 'snel'), zou de rustmassa van die deeltjes, m₀, imaginair moeten zijn; voor v > c zou de massa m dan de verhouding van twee imaginaire getallen zijn en daardoor een reële waarde hebben. Voor zulke hypothetische deeltjes zou c de ondergrens van de snelheid zijn. Er is intensief naar tachyonen gezocht, maar tot nu toe is er nooit een gevonden. Naar het zich laat aanzien is de lichtsnelheid dus inderdaad de hoogst mogelijke snelheid in het heelal.
terug naar de Inhoud

40-11 E = mc² - Massa en energie
Wanneer er op een voorwerp met rustmassa m₀ een constante nettokracht wordt uitgeoefend, neemt de snelheid van dat voorwerp toe. Daar de kracht werkzaam is over een afstand, wordt er aan het voorwerp arbeid verricht, zodat de energie van het voorwerp toeneemt. De snelheid van het voorwerp nadert daarbij tot de lichtsnelheid c, maar kan niet onbepaald toenemen, want de snelheid kan nooit groter worden dan c. Aan de andere kant wordt, naarmate de snelheid van het voorwerp toeneemt, ook de massa groter.
Dat wil zeggen, als gevolg van de arbeid die aan een voorwerp wordt verricht, neemt niet alleen de snelheid toe, maar wordt ook de massa vergroot. Gewoonlijk neemt de energie van een voorwerp toe als er arbeid aan verricht wordt. Deze nieuwe wending uit de relativiteitstheorie geeft aanleiding tot het idee dat massa een vorm van energie is en dit inzicht vormt een cruciaal onderdeel van Einsteins relativiteitstheorie.
De totale energie van een deeltje dat in rust verkeert, bedraagt E = m₀c², een waarde die we de rustenergie van het deeltje hebben genoemd. Deze vergelijking geeft het wiskundige verband tussen de begrippen energie en massa. Dit idee heeft echter slechts dan praktische betekenis, als het ook werkelijk mogelijk is massa in energie om te zetten en omgekeerd. Dat wil zeggen, als massa alleen maar een vorm van energie is, zou het mogelijk moeten zijn massa om te zetten in andere vormen van energie, net zoals ook die andere vormen van energie onderling uitwisselbaar zijn. Einstein was van mening dat zo'n omzetting wellicht mogelijk was, en dat bleek inderdaad het geval: dat massa en energie in elkaar kunnen worden omgezet, is sindsdien op talloze manieren experimenteel bevestigd en we kennen tegenwoordig veel belangrijke processen die op zo'n omzetting zijn gebaseerd.

Omzettingen tussen massa en energie zijn het gemakkelijkst aan te tonen in processen uit de kernfysica en de elementaire deeltjesfysica. Zo blijkt het neutrale pion (π₀) dat een rustmassa heeft van 2,4 x 10^-28 kg tot uitsluitend elektromagnetische straling (fotonen) te vervallen, waarbij het deeltje zelf volledig verdwijnt. De hoeveelheid elektromagnetische energie die daarbij vrijkomt, blijkt overeen te stemmen met de formule van Einstein, E = m₀c². Ook het omgekeerde proces is in het laboratorium gemakkelijk te demonstreren: in bepaalde omstandigheden kan elektromagnetische straling worden omgezet in materiedeeltjes, zoals elektronen.
Een grootschalig voorbeeld van processen waarin massa in energie wordt omgezet, zijn de kernsplijtingsprocessen in kerncentrales; de massa die bij splijting van het uranium verloren gaat, levert de energie van zo 'n centrale. Ook de stralingsenergie die door de zon wordt geleverd, ontstaat door omzetting van massa in energie; terwijl de zon alsmaar energie uitstraalt, wordt de massa van de zon kleiner.
terug naar de Inhoud

40-12 De invloed van de speciale relativiteitstheorie op ons wereldbeeld
De voorspellingen die uit de speciale relativiteitstheorie volgen, zijn in talloze experimenten getoetst en zij geven allemaal resultaten die overeenstemmen met de theorie. Natuurkundigen hebben deze theorie daarom in overgrote meerderheid geaccepteerd als een correcte beschrijving van de natuur.
Zoals is besproken gaan de relativistische formules over in de vertrouwde formules van de klassieke mechanica wanneer de snelheden klein zijn in vergelijking met de lichtsnelheid en dat mogen we natuurlijk ook wel verwachten, want de mechanica van Newton is volkomen bevredigend waar het gaat om voorwerpen die zich verplaatsen met snelheden die veel kleiner zijn dan de lichtsnelheid. De eis dat een meer algemene theorie zoals de relativiteitstheorie, dezelfde uitkomsten geeft als een meer beperkte theorie zoals de klassieke mechanica, die heel goed werkt voor v << c, wordt het correspondentieprincipe genoemd. Waar het geldigheidsgebied van de ene theorie dat van de andere overlapt, moeten die theorieën gelijkluidende uitkomsten geven. De relativiteitstheorie is niet in tegenspraak met de klassieke mechanica; het is een meer algemene theorie en de klassieke mechanica geldt tegenwoordig als een bijzonder geval.

Het belang van de relativiteitstheorie is niet alleen dat zij, met name waar het gaat om zeer hoge snelheden, nauwkeurigere uitkomsten geeft. Belangrijker is dat zij ons wereldbeeld ingrijpend heeft gewijzigd. Tijd en ruimte worden nu als relatief gezien en als nauw met elkaar vervlochten begrippen beschouwd, terwijl tijd en ruimte vóór de relativiteitstheorie als absolute en gescheiden begrippen golden. Ook onze begrippen energie en materie ondergingen verandering: energie en massa blijken in elkaar te kunnen worden omgezet. De invloed van de relativiteitstheorie strekt zich uit tot ver buiten de natuurkunde. De theorie heeft ook invloed gehad op andere wetenschappen en zelfs op de wereld van kunst en litteratuur, en heeft op die manier de hele cultuur beïnvloed.
Vanuit een louter praktisch standpunt bezien, helpt de wiskunde van de relativiteit ons in het dagelijkse leven weinig verder. Waar het om snelheden kleiner dan 0,1 c gaat en in situaties waarin er geen omzetting tussen massa en energie plaatsvindt, is het gewoonlijk niet nodig de verhoudingsgewijs ingewikkelde formules van de relativiteitstheorie te gebruiken en kan er worden volstaan met de eenvoudiger formules van de klassieke mechanica.
terug naar de Inhoud

Samenvatting
Een inertiaal referentiestelsel is een referentiestelsel waarin de traagheidswet van Newton geldt: zij verkeren in rust. Inertiaalstelsels kunnen zich met een constante snelheid ten opzichte van elkaar verplaatsen; referentiestelsels die versnelling ondergaan zijn niet inertiaal.
De speciale relativiteitstheorie van Einstein rust op twee uitgangspunten:
(1) het relativiteitsprincipe, dat zegt dat in elk inertiaalstelsel dezelfde natuurwetten gelden, en
(2) het postulaat van de constante lichtsnelheid, dat stelt dat de lichtsnelheid in lege ruimte in elk inertiaalstelsel dezelfde waarde heeft.

Een aantal inzichten van de relativiteitstheorie is:
- twee gebeurtenissen die in een gegeven referentiestelsel gelijktijdig zijn, niet noodzakelijk ook gelijktijdig zijn in een ander referentiestelsel;
- het bestaan van tijddilatatie: klokken die worden verplaatst, blijken langzamer te lopen; de tijd wordt uitgerekt;
- het voorkomen van lengtecontractie: wanneer een voorwerp wordt verplaatst, is het voorwerp gemeten in de richting waarin het wordt verplaatst korter dan wanneer het in rust verkeert;
- massatoename: de massa van een voorwerp is groter naarmate de snelheid groter is.
Al deze effecten zijn alleen van belang bij hoge snelheden, in de buurt van de lichtsnelheid, de hoogste snelheid die in het heelal mogelijk is. De relativiteitstheorie heeft onze opvattingen van ruimte en tijd, en van massa en energie ingrijpend veranderd:
- ruimte en tijd zijn nauw met elkaar verweven: zij vormen een vierdimensionaal stelsel waarin tijd de vierde dimensie is;
- massa en energie kunnen in elkaar worden omgezet;
- de vergelijking E = mc² geeft de hoeveelheid energie E, die nodig is om een hoeveelheid massa m te vormen (of omgekeerd weer om te zetten);
- in de wet van behoud van energie moet massa als een vorm van energie worden gerekend.
terug naar de Inhoud

Hoofdstuk 41- De vroege quantumtheorie

Inleiding
De revolutie die in het begin van de twintigste eeuw in de natuurkunde plaatsvond, speelde zich af op twee fronten: de eerste omwenteling was de relativiteitstheorie van Einstein en de tweede het onderwerp van dit hoofdstuk: het ontstaan van de quantumtheorie. Werden de grondbeginselen van de speciale relativiteitstheorie in hoofdzaak binnen een tijdsbestek van slechts één jaar door één persoon ontwikkeld, de ontwikkeling van de quantumtheorie strekte zich over bijna drie decennia uit en veel natuurkundigen hebben eraan bijgedragen. Deze ontwikkeling begon in 1900 met de quantumhypothese van Planck en beleefde haar hoogtepunt in het midden van de jaren twintig toen Schrödinger en Heisenberg de theorie van de quantummechanica formuleerden, een theorie die buitengewoon veel succes heeft gehad bij het verklaren van de structuur van materie.
terug naar de Inhoud

41-1 De quantumhypothese van Planck
Planck stelde een formule op voor de elektromagnetische straling van hete voorwerpen; in een denkbeeldige vorm worden zij 'zwarte lichamen' genoemd. Een zwart lichaam is een lichaam waarvan wordt uitgegaan dat het alle straling die erop valt, absorbeert (dit om het rekenen eraan te vergemakkelijken); de straling die zo'n lichaam vervolgens zelf uitzendt, wordt 'zwarte straling' genoemd.
Daarna zocht hij een theoretische grondslag voor zijn formule en ontdekte binnen twee maanden dat hij de formule kon afleiden door een nieuwe en radicale aanname te maken (het radicale daarvan werd overigens pas later ingezien): Planck nam aan dat de energie die door moleculaire oscillatoren wordt uitgezonden, niet continu is, maar uit een eindig aantal zeer kleine, discrete hoeveelheden bestaat. Het verband tussen de hoeveelheid energie en de frequentie wordt gegeven door de formule: E = hf (h is de constante van Planck). De aanname van Plank is, dat de energie van elke moleculaire trilling altijd een geheel veelvoud van hf is: E = nhf, waarbij n = 1, 2, 3...

De quantumhypothese zoals we die tegenwoordig kennen, zegt dat de energie E, gelijk kan zijn aan hf, 2hf, 3hf, enzovoort, maar dat er geen trillingen mogelijk zijn met een energie die tussen deze waarden inligt. Energie bleek dus, anders dan eeuwenlang was aangenomen, geen continue grootheid te zijn; energie is gequantiseerd of anders gezegd: energie bestaat alleen in discrete hoeveelheden. De kleinst mogelijke hoeveelheid energie (hf) wordt een 'energiequantum' genoemd. Op een wat andere manier geformuleerd zegt de quantumhypothese dat niet elke trillingsamplitude mogelijk is. Welke waarden de amplitude kan aannemen hangt af van de frequentie f.
terug naar de Inhoud

41-2 De theorie van lichtfotonen en het foto-elektrische effect
Einstein kwam in 1905, het jaar waarin bij ook de speciale relativiteitstheorie publiceerde, met een stoutmoedige uitbreiding van het quantumidee. Hij stelde een nieuwe lichttheorie voor. In het werk van Planck werd aangenomen dat de trillingsenergie van de moleculen in een stralend voorwerp gequantiseerd is volgens E = nhf. Einstein redeneerde als volgt: als de energie van de moleculaire oscillatoren op de bovenbeschreven manier is gequantiseerd, moet de energie van een moleculaire oscillator die licht uitzendt daarbij minstens met een waarde hf verminderen; als de energie van de oscillator oorspronkelijk nhf was, wordt die energie na uitzending van het licht (n-1)hf. Wil er worden voldaan aan de wet van behoud van energie, dan moet ook licht worden uitgezonden in pakketjes of quanta, met elk een energie E = hf.
Alle licht komt uiteindelijk van een stralingsbron en dat wekt het vermoeden dat licht mogelijk niet in de vorm van golven wordt verstuurd, maar in de vorm van zeer kleine deeltjes of, zoals we tegenwoordig zeggen, fotonen. Ook deze gedachte vormde een radicale afwijking van de klassieke inzichten. Einstein stelde een eenvoudig experiment voor, waarmee de quantumtheorie van licht zou kunnen worden getoetst: de kwantitatieve meting van het foto-elektrische effect.

Volgens de theorie van Einstein wordt bij het foto-elektrische effect een elektron uit het metaal weggestoten door botsing met één foton uit het invallende licht. Bij dit botsingsproces wordt alle energie van het foton overgedragen op het elektron en daarbij houdt het foton op te bestaan. Omdat de elektronen in het metaal door aantrekkingskrachten worden vastgehouden, vereist het een bepaalde minimum hoeveelheid energie W₀ (de uittreedarbeid, die voor de meeste metalen enkele elektronvolts bedraagt) om een elektron uit het metaaloppervlak los te maken. Als de frequentie f van het invallende licht zo laag is, dat hf kleiner is dan W₀, hebben de fotonen niet voldoende energie om ook maar één elektron vrij te maken. Is hf > W₀, dan worden er wel elektronen vrijgemaakt en daarbij blijft de energie behouden. Dat wil zeggen, de toegevoerde energie van het foton, hf, is gelijk aan de kinetische energie KE van het vrijgemaakte elektron plus de energie W die nodig is om het elektron uit het metaal te bevrijden: hf = KE + W. In het geval van de elektronen die het zwakst aan het metaal zijn gebonden, is W de uittreedarbeid W₀ en de KE in deze vergelijking, KE_max is dan: hf = KE_max + W₀.
De meeste elektronen zijn sterker gebonden en het vraagt daardoor meer energie om zulke elektronen net uit het metaal los te maken dan de minimum hoeveelheid, W₀ en de kinetische energie die zulke elektronen krijgen is daardoor kleiner dan het maximum.
Op grond van bovenstaande overwegingen komt de fotonentheorie tot de volgende voorspellingen:
1. Naarmate de intensiteit van de lichtbundel hoger is, wordt het metaal door een groter aantal fotonen getroffen en worden er meer elektronen vrijgemaakt; maar aangezien de energie van de afzonderlijke fotonen gelijk blijft, blijft ook de maximale kinetische energie van de vrijgekomen elektronen gelijk.
2. De maximale kinetische energie van de elektronen is recht evenredig aan de frequentie van het licht: KE_max = hf - W₀
3. Is de frequentie f lager dan de 'afsnij'frequentie f₀, gegeven door hf₀ = W₀, dan worden er geen elektronen vrijgemaakt.

Het is duidelijk dat de voorspellingen van de fotonentheorie sterk verschillen van die van de golftheorie. In 1913-1914 werden er door R.A. Millikan nauwkeurige experimenten gedaan en de uitkomsten kwamen overeen met de voorspellingen van de fotonentheorie van Einstein.
Er was nog een ander aspect van het foto-elektrische effect dat in overeenstemming bleek met de fotonentheorie. De golftheorie voorspelt dat er een vertragingseffect optreedt, wanneer er licht van een uiterst geringe intensiteit wordt gebruikt. In dat geval duurt het namelijk enige tijd voordat de elektronen een hoeveelheid energie hebben geabsorbeerd die groter is dan de uittreedarbeid. De fotonentheorie daarentegen voorspelt hier geen vertraging, want er is maar één foton (van voldoende frequentie) nodig om één elektron vrij te maken. In experimenten werd geen vertraging gevonden en ook dit bevestigt de fotonentheorie van Einstein.
terug naar de Inhoud

41-4 Wisselwerkingen tussen fotonen - Paarvorming
Wanneer een foton zich door materie verplaatst, treedt het in wisselwerking met de atomen en elektronen ervan. Het foton kent vier belangrijke vormen van interactie:
- ten eerste kan het door botsing met een elektron (of een atoomkern) worden afgebogen en verliest daarbij dan wat energie: dit is het Compton effect; merk echter op dat het foton niet vertraagd wordt, het behoudt zijn snelheid c, maar de frequentie is na de botsing verminderd;
- een tweede vorm van interactie is het foto-elektrische effect; een foton kan een elektron uit een atoom doen ontsnappen en houdt daarbij dan zelf op te bestaan;
- de derde vorm lijkt op het tweede: een foton dat niet voldoende energie heeft om een elektron uit een atoom vrij te maken, kan een elektron binnen het atoom in een hogere energietoestand brengen; ook in dit geval houdt het foton op te bestaan en wordt alle energie ervan opgenomen door het atoom; zo'n atoom raakt dan in een zogenaamde 'aangeslagen toestand', een onderwerp waarop we later nog terugkomen;
- tenslotte kan een foton materie doen ontstaan. Het bekendste voorbeeld van een dergelijk proces is de vorming van een elektron en een positron. Een positron heeft dezelfde massa als een elektron, maar een tegengestelde lading, +e en wordt het antideeltje van het elektron genoemd. In de natuur is het positron geen lang leven beschoren, want het botst al snel met een elektron. Wanneer dit gebeurt, vernietigen beide deeltjes elkaar (annihilatie) en produceren twee of meer fotonen. Ook dit paarsgewijze annihilatieproces voldoet aan E = mc².

Bij het vormingsproces, dat paarvormig wordt genoemd, houdt het foton op te bestaan. We zien hier een voorbeeld van een proces waarbij uit zuivere energie rustmassa ontstaat. De betrokken hoeveelheden energie en massa blijken te voldoen aan de vergelijking van Einstein, E = mc². Merk op dat er uit een foton nooit alleen een elektron kan ontstaan, want dat zou in strijd zijn met de wet van behoud van elektrische lading.
Paarvorming kan niet plaatsvinden in lege ruimte want indien dat wel gebeurde, zouden niet tegelijk zowel energie als impuls behouden kunnen blijven. Zo blijft bij paarvorming de energie behouden, maar in tegenstelling tot het oorspronkelijke foton hebben het elektron en positron in ons voorbeeld geen impuls. Er kan dan ook worden aangetoond dat ongeacht de energie van het foton er altijd nog een extra, massief object (zoals een atoomkern) aan het proces moet deelnemen om een deel van de impuls van het foton over te nemen.
terug naar de Inhoud

41-5 De golfdeeltje-dualiteit - Het principe van complementaire voorstellingen
Het foto-elektrische effect, het Compton effect en andere experimenteel waargenomen verschijnselen geven de deeltjestheorie van licht een stevige empirische basis. Maar hoe zit het dan met de klassieke experimenten van Young en anderen met betrekking tot interferentie en buiging? Deze proefnemingen hebben immers laten zien dat ook de golftheorie van licht een zelfde experimentele basis heeft!
We lijken verstrikt te zijn geraakt in een dilemma. Sommige experimenten geven aan dat licht zich als een golf gedraagt, andere proeven laten daarentegen zien dat licht zich gedraagt als een stroom van deeltjes. Hoewel deze twee theorieën onverenigbaar lijken, blijken ze toch beide te gelden. Natuurkundigen zijn uiteindelijk tot de conclusie gekomen dat we deze tweeslachtigheid van licht als een onvermijdelijk feit moeten aanvaarden. Met spreekt in dit verband van dualiteit. Blijkbaar is licht een ingewikkelder verschijnsel dan alleen maar een eenvoudige golf of alleen maar een eenvoudige bundel deeltjes.

Teneinde de situatie te verhelderen formuleerde de grote Deense natuurkundige Niels Bohr (1885-1962) het beroemd geworden principe van complementaire voorstellingen. Dit principe zegt dat we om een gegeven experiment te begrijpen óf de golftheorie óf de fotonentheorie moeten gebruiken, maar niet beide. Niettemin dienen we ons - teneinde het verschijnsel licht volledig te kunnen begrijpen - te realiseren dat licht zowel golf- als deeltjesaspecten heeft. De beide aspecten van licht lijken elkaar aan te vullen.
We zijn niet in staat ons deze golfdeeltje-dualiteit in een visueel model voor te stellen en kunnen golf en deeltje niet in een beeld verenigen: door zich dan weer als golf, dan weer als deeltjes te gedragen, toont licht de onderzoeker afwisselend twee verschillende 'gezichten'.

Een deel van de moeilijkheid komt voort uit de manier waarop we denken. De visuele beelden of modellen die de menselijke geest weet voort te brengen, zijn ontleend aan onze alledaagse ervaring. Een 'model' is een soort analogie of denkbeeldige voorstelling waarin we iets wat ons vertrouwd is, gebruiken om een verzameling samenhangende verschijnselen te beschrijven die zich afspelen op een niveau, dat zich aan directe waarneming onttrekt. We maken gebruik van de begrippen golven en deeltjes omdat we in de macroscopische wereld zien dat energie op die twee manieren van de ene naar de andere plaats kan worden getransporteerd. We kunnen echter niet op een directe manier zien of licht een deeltje dan wel een golf is en daarom doen we indirecte experimenten.
Om de uitkomsten van onze proeven te verklaren, passen we op licht het golfmodel of het deeltjesmodel toe. Beide modellen zijn echter abstracties van de menselijke geest. Wanneer we proberen te begrijpen wat licht werkelijk is, verlangen we een visueel beeld. Maar in feite is er volstrekt geen reden waarom licht zou moeten voldoen aan modellen (of beelden) die zijn ontleend aan de macroscopische wereld. De ware aard van licht kan niet als beeld worden voorgesteld. Het beste wat we kunnen doen is te onderkennen dat onze kennis zich beperkt tot indirecte experimenten en dat licht - in termen van alledaagse voorstellingen en alledaags spraakgebruik - zowel kenmerken van golven als van deeltjes heeft.
Het is veelzeggend dat ook in Einsteins vergelijking E = hf zowel het deeltjeskarakter als de golfeigenschappen van licht aanwezig zijn: in deze vergelijking is E de energie van een deeltje en in de uitdrukking rechts van het is gelijk-teken staat de frequentie f van de corresponderende golf.
terug naar de Inhoud

41-6 Het golfkarakter van materie
In 1923 kreeg het begrip golf-deeltjedualiteit een bredere toepassing dankzij het werk van Louis de Broglie (1892-1987). De Broglie, die een sterk geloof had in de symmetrie van de natuur, opperde dat behalve licht mogelijk ook andere bouwstenen van de natuur die tot nu toe altijd als deeltjes waren beschouwd (zoals elektronen, protonen en neutronen) zich in sommige omstandigheden als golf gedragen. De Broglie kwam met de hypothese dat het verband tussen de golflengte van een deeltje materie en de impuls van dat deeltje net als in het geval van een foton gegeven wordt door vergelijking p = h/λ. Dat wil zeggen, de golflengte λ van een deeltje met massa m dat zich verplaatst met een snelheid v, wordt gegeven door: λ = h/mv. Deze golflengte wordt wel de 'De Broglie golflengte van een deeltje' genoemd.
Dit is een uiterst kleine golflengte. Zelfs als de snelheid van een kogel zeer gering is, bijvoorbeeld 10^-4m/s, zou de golflengte slechts 10^-29 m zijn. De golflengte van een gewoon voorwerp is dan ook veel te klein om te worden waargenomen. Het probleem is dat de eigenschappen van golven, zoals interferentie en buiging, alleen van belang zijn wanneer de betrokken voorwerpen of spleten niet veel groter zijn dan de golflengte. We kennen geen voorwerpen of spleten die in staat zijn golven af te buigen waarvan de golflengte slechts 10^-30 m bedraagt en daarom merken we niets van de golfeigenschappen van gewone voorwerpen.
Maar met zeer kleine elementaire deeltjes, zoals elektronen, ligt de zaak anders: de massa m staat in de vergelijking λ = h/mv in de noemer en dat betekent dat de golflengte bij een zeer kleine massa veel groter is.
Elektronen kunnen golflengten hebben van de orde van grootte van 10^-10 m. Zo'n golflengte is erg klein, maar kan wel gedetecteerd worden, want de afstand tussen de atomen in een kristal is van de orde van grootte van 10^-10 m. Daardoor kan een kristalrooster hier als buigingsrooster worden gebruikt, net zoals dat eerder gebeurde bij röntgenstralen. Het doorslaggevende experiment werd uitgevoerd door C.J. Davisson en L.H. Germer. Begin 1927 merkten ze op dat elektronen na te zijn verstrooid door botsing met het oppervlak van een metaalkristal een regelmatig patroon van maxima gaven en toen ze de waargenomen pieken als buigingspatroon interpreteerden, vonden ze als golflengte van de afgebogen elektronengolf precies de golflengte die door de De Broglie vergelijking was voorspeld. In datzelfdejaar nam ook G.P. Thomson buiging van elektronen waar in een experiment dat anders van opzet was dan dat van Davisson en Germer. Uit latere proeven is gebleken dat ook protonen, neutronen en andere deeltjes golfeigenschappen bezitten.

Dualiteit is niet alleen een kenmerk van licht: ook stoffelijke voorwerpen hebben zowel kenmerken van golven als van deeltjes en het principe van complementaire voorstellingen is ook van toepassing op materie. Dat wil zeggen, voor een juist begrip van materie (zoals elektronen en protonen) moeten we in het oog houden dat materie zowel kenmerken van golven als van deeltjes heeft, maar ook hier moeten we erkennen dat we ons een 'golfdeeltje' niet als visueel beeld kunnen voorstellen.

We kunnen ons de vraag stellen: "Wat is een elektron?" In de vroege experimenten van J.J. Thomson werd er in een vacuümbuis een gloed waargenomen die met behulp van een magnetisch veld kon worden verplaatst. De effecten die zich in dit experiment en in nog andere proeven voordeden, lieten zich het beste verklaren door het bestaan aan te nemen van zeer kleine negatief geladen deeltjes, die nu elektronen worden genoemd. Geen mens heeft echter ooit werkelijk op een directe manier een elektron gezien. De elektronen zoals die in sommige van onze tekeningen figureren - kleine bolletjes voorzien van een minteken dat de negatieve lading aangeeft - zijn niet meer dan denkbeeldige voorstellingen die, zoals we nu weten, niet met de werkelijkheid overeenkomen. Het enige waarover we beschikken zijn de uitkomsten van onze experimenten, waarvan sommige zich het beste laten interpreteren aan de hand van het deeltjesmodel en andere beter aan de hand van het golfmodel.
Deze modellen zijn echter niet meer dan voorstellingen die we ontlenen aan de macroscopische wereld en nu proberen toe te passen op de uiterst kleinschalige wereld van het atoom. Er is geen reden om aan te nemen dat deze modellen op de een of andere manier de realiteit van het elektron weergeven. Door gebruik te maken van een golf- of deeltjesmodel, afhankelijk van wat in de gegeven situatie het beste werkt, zijn we in staat om over de verschijnselen te praten. We zouden ons er niet toe moeten laten verleiden te gaan geloven dat een elektron een golf of een deeltje is. Op de vraag "wat is een elektron" kunnen we antwoorden dat een elektron de verzameling is van eigenschappen die we kunnen meten. Bertrand Russell sloeg de spijker op zijn kop toe hij schreef dat een elektron een 'logische constructie' is.
terug naar de Inhoud

Hoofdstuk 42 - Quantummechanica

Inleiding
Met het atoommodel van Bohr beschikte men voor het eerst over een (onvolledige) voorstelling van het atoom. Dit model bood een verklaring voor de stabiliteit van atomen en wist ook te verklaren, waarom een atoom alleen licht van bepaalde, discrete golflengten absorbeert en uitzendt. Berekenen we voor waterstof en voor ionen met één elektron in de buitenste schil op basis van het model van Bohr de ionisatie-energie en de golflengten van de lijnenspectra, dan vinden we uitkomsten die nauwkeurig overeenstemmen met de experimentele gegevens.
Toch had de theorie van Bohr ook ernstige tekortkomingen. Het was met deze theorie bijvoorbeeld niet mogelijk de lijnenspectra van ingewikkeldere atomen te voorspellen, zelfs niet die van neutraal helium, dat toch slechts twee elektronen bezit. De theorie kon ook niet verklaren waarom elk van de emissielijnen in feite niet uit één lijn bestaat, maar uit twee of meer lijnen die zeer dicht bij elkaar liggen - een verschijnsel dat de fijnstructuur wordt genoemd. Verder gaf de theorie van Bohr geen verklaring voor het feit dat sommige spectraallijnen duidelijker zijn dan andere en de theorie bood al evenmin een verklaring voor de binding van atomen in moleculen, vaste stoffen en vloeistoffen. Ook vanuit theoretisch oogpunt was Bohrs theorie niet erg bevredigend, want het was een vreemd mengsel van klassieke inzichten en quantumideeën en bood in feite geen oplossing voor het probleem van de golfdeeltje-dualiteit.

Deze opsomming van beperkingen is overigens niet bedoeld om Bohrs prestatie te kleineren, want zijn theorie was een mijlpaal in de geschiedenis van de natuurkunde. We noemen al die tekortkomingen om duidelijk te maken waarom er in het begin van de jaren twintig steeds meer behoefte ontstond aan een nieuwe, bredere theorie. Deze liet niet lang op zich wachten, want nog geen twee jaar nadat De Broglie met zijn materiegolfhypothese was gekomen, ontwikkelden Erwin Schrödinger (1887-1961) en Werner Heisenberg (1901-1976) onafhankelijk van elkaar een nieuwe en complete theorie. Hoewel ze elk een heel andere weg hadden gekozen, bleek al snel dat de twee theorieën volledig op elkaar aansloten; ze vormen samen een geheel, de quantummechanica, het onderwerp van dit hoofdstuk.
terug naar de Inhoud

42-1 Quantummechanica: een nieuwe theorie
In de quantummechanica zijn het golf- en deeltjesaspect van elementaire deeltjes in een consistente theorie samengebracht. De quantummechanica is een buitengewoon succesvolle theorie gebleken, die de emissiespectra van ingewikkelde atomen tot in de fijnste details weet te verklaren en ook kan uitleggen hoe de helderheidsverschillen tussen spectraallijnen ontstaan en hoe atomen moleculen vormen ('chemische binding'). Bovendien is deze theorie veel algemener dan die van Bohr, want de quantummechanica heeft betrekking op alle quantumverschijnselen, uiteenlopend van de straling van zwarte lichamen tot aan de structuur van en de interactie tussen atomen en moleculen. Met de quantumtheorie kan dus een brede verscheidenheid van natuurlijke verschijnselen worden verklaard en de voorspellingen van deze theorie hebben geleid tot allerlei nieuwe technische ontwikkelingen. Dit grote succes heeft ertoe geleid dat de quantumtheorie tegenwoordig door vrijwel alle natuurkundigen wordt aanvaard als de fundamentele theorie achter fysische processen.

De quantummechanica houdt zich hoofdzakelijk bezig met de zeer kleinschalige wereld van atomen en lichtquanta. Maar ook in onze macroscopische wereld van alledag hebben we met licht te maken en we weten dat gewone voorwerpen uit atomen zijn opgebouwd. De quantummechanica moet dus aansluiten bij de resultaten die de klassieke natuurkunde heeft opgeleverd. Dat wil zeggen, indien toegepast op macroscopische verschijnselen, dient de quantummechanica tot de klassieke natuurwetten te leiden. Aan deze eis, het zogenaamde correspondentieprincipe (dat al ter sprake kwam in par. 41-10), wordt door de quantummechanica volledig voldaan. Dit betekent echter niet dat we de klassieke theorieën nu overboord gooien, want de klassieke wetten geven een nauwkeurige beschrijving van de alledaagse wereld en laten zich veel makkelijker toepassen dan quantummechanica. Wanneer we echter te maken hebben met hoge snelheden, in de buurt van de lichtsnelheid, moeten we de relativiteitstheorie gebruiken en waar het gaat om de zeer kleine wereld van het atoom, gebruiken we quantummechanica.

In het volgende bespreken we - zonder diep op de wiskunde in te gaan - de belangrijkste inzichten van de quantummechanica en laten dan onder meer zien hoe men op basis van deze inzichten, door rekening te houden met zowel de golf- als de deeltjeseigenschappen van materie, de opbouw van atomen kan verklaren.
terug naar de Inhoud

42-2 De golffunctie en haar interpretatie - Het dubbelspleetexperiment
Elke golf wordt gekarakteriseerd door: golflengte λ, frequentie f en amplitude a;

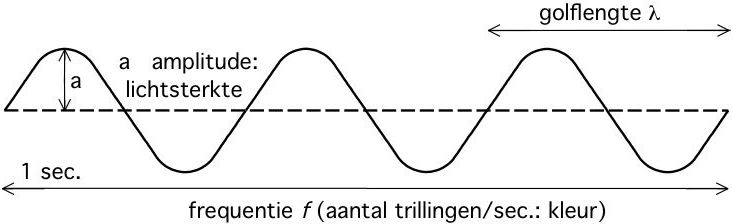- zoals we hebben gezien hangt het van de golflengte van een elektromagnetische golf af, of de golf al dan niet zichtbaar is als licht en zo ja welke kleur het licht dan heeft;
- verder hebben we in hoofdstuk 41 gezien dat de golflengte (ofwel de frequentie) een maat is voor de energie van het corresponderende foton: E = hf;
- de amplitude (de uitwijking) van een elektromagnetische golf in een willekeurig punt is de sterkte van het elektrische (of magnetische) veld in dat punt en hangt samen met de intensiteit van de golf (de helderheid van het licht).

In het geval van materiedeeltjes zoals elektronen, volgt het verband tussen golflengte en impuls uit de quantummechanica en wordt gegeven door de formule van De Broglie, λ = h/mv. Maar wat correspondeert met de amplitude (dus met de uitwijking) van een materiegolf? In de quantummechanica wordt deze grootheid weergegeven door de golffunctie, aangegeven met het symbool Ψ (de Griekse hoofdletter Psi). De golffunctie Ψ geeft de amplitude van een nieuw soort veld als functie van tijd en plaats, een veld dat we een 'materieveld' of een 'materiegolf' kunnen noemen.

Berekening van de golffunctie Ψ voor gegeven situaties (bijvoorbeeld voor een elektron in een atoom) is een van de hoofdtaken van de quantummechanica. De natuurkundige Erwin Schrödinger ontwikkelde een vergelijking die zulke berekeningen mogelijk maakt en leverde daarmee een hoogst belangrijke bijdrage aan de quantummechanica. De 'golfvergelijking van Schrödinger', zoals deze wordt genoemd, geldt als de basisvergelijking voor de beschrijving van niet relativistische materiedeeltjes. We zullen de vergelijking van Schrödinger en enkele oplossingen daarvan voor een paar eenvoudige gevallen later in dit hoofdstuk nog bespreken. We vragen ons nu eerst het volgende af: hoe moeten we de golffunctie Ψ voor een deeltje interpreteren? Een van de mogelijkheden is Ψ eenvoudigweg op te vatten als de uitwijking van een 'materiegolf' in een willekeurig punt in ruimte en tijd; we wezen daar al eerder op en Ψ speelt dan dezelfde rol als E (de elektrische veldsterkte) in een elektromagnetische golf. We zullen dit nu verder verduidelijken door een vergelijking te trekken met licht.

De intensiteit I van een mechanische golf is altijd evenredig aan het kwadraat van de amplitude. Dit geldt ook voor lichtgolven en zoals in hoofdstuk 34 werd uitgelegd, is de energiedichtheid in een lichtgolf evenredig aan E², waarin E de elektrische veldsterkte is. Beschouwen we licht als een stroom van deeltjes, dan is de energiedichtheid van een lichtbundel evenredig aan het aantal fotonen n per eenheid van volume. Hoe groter het aantal fotonen (van een gegeven golflengte) per eenheid van volume, des te groter is de energiedichtheid van de bundel. Er geldt dus n ~ E². Dat wil zeggen, het aantal fotonen per eenheid van volume is evenredig aan het kwadraat van de elektrische veldsterkte.

Als de lichtbundel zeer zwak is, gaat het slechts om enkele fotonen. Door zeer zwak licht te gebruiken is het dus mogelijk bijvoorbeeld een foto heel langzaam 'op te bouwen', zodat het effect van afzonderlijke fotonen te zien is. Hebben we te maken met slechts één foton, dan kunnen we de boven gegeven vergelijking (n ~ E²) op een iets andere manier interpreteren. In elk punt is het kwadraat van de elektrische veldsterkte E², een maat voor de waarschijnlijkheid dat er in een eenheid van volume op die plaats een foton wordt aangetroffen. Anders gezegd, als Δ.V een infinitesimaal volume element om het betreffende punt is, is E²Δ.V evenredig aan de kans binnen het volume Δ.V een foton te vinden. De kans het foton aan te treffen is groot in punten waarin E² groot is en klein in punten waarin E² klein is.

Materiegolven laten zich op dezelfde manier interpreteren. De grootte van de golffunctie Ψ kan in de ruimte (dus van punt tot punt) en in de tijd variëren.
1. Als Ψ een verzameling van een groot aantal elektronen beschrijft, is |Ψ|²Δ.V evenredig aan het te verwachten aantal elektronen in het volume Δ.V rond een gegeven punt.
2. Hebben we te maken met een klein aantal elektronen, dan kunnen we geen nauwkeurige voorspellingen meer doen en krijgt |Ψ|² het karakter van een waarschijnlijkheid.
3. Als de golffunctie Ψ, die zowel van tijd als van plaats afhangt, één elektron weergeeft (bijvoorbeeld een elektron in een atoom), wordt |Ψ|² als volgt geïnterpreteerd: in een willekeurig punt in ruimte en tijd geeft ΨΔ.V de waarschijnlijkheid het elektron op het betreffende tijdstip aan te treffen in het volume Δ.V om het gegeven punt. Daarbij wordt |Ψ|² de waarschijnlijkheidsdichtheid (of ook wel de waarschijnlijkheidsverdeling) genoemd, want |Ψ|² is de waarschijnlijkheid het deeltje aan te treffen per eenheid van volume.

Ter verduidelijking bekijken we aan de hand van de quantummechanica het bekende dubbelspleetexperiment, voor zowel licht als voor elektronen. Stel dat we twee spleten hebben en dat de breedte van die spleten en hun onderlinge afstand van dezelfde orde van grootte zijn als de golflengte van de licht- of elektronenbundel die we erop afsturen. Wat er in dit geval met licht gebeurt weten we al, want dit is het dubbelspleetexperiment van Young: op het scherm achter de spleet ontstaat een interferentiepatroon doordat golven elkaar afwisseld versterken of uitdoven. Vervangen we het licht door elektronen met een golflengte die vergelijkbaar is met de breedte van een spleet, dan verkrijgen we eveneens een interferentiepatroon. Het interferentiepatroon dat ontstaat wanneer we licht gebruiken, is direct zichtbaar of kan worden gefotografeerd. Wanneer we elektronen gebruiken, kan het patroon zichtbaar worden gemaakt met een fluorescentiescherm, dat opgloeit waar het getroffen wordt door een elektron.
Wanneer we de toevoer van elektronen (of van fotonen) verminderen, zodat er gemiddeld slechts één tegelijk door de spleten gaat, zien we telkens wanneer een elektron het scherm treft een lichtflits. In het begin zullen we de flitsjes zien op willekeurige plaatsen, want het is fundamenteel onmogelijk te voorspellen waar elk afzonderlijk elektron het scherm zal treffen. Maar als we het experiment een lange tijd voortzetten en ondertussen bijhouden waar de verschillende elektronen op het scherm botsen, zien we al snel een patroon ontstaan - namelijk het interferentiepatroon dat voorspeld wordt door de golftheorie. Hoewel we niet kunnen voorspellen waar een gegeven elektron het scherm zal treffen, kunnen we dus wel waarschijnlijkheden voorspellen; hetzelfde geldt voor fotonen. Zoals eerder werd vermeld, is de waarschijnlijkheid evenredig aan |Ψ|². Op plaatsen waar |Ψ|² nul is, ontstaat er een minimum in het interferentiepatroon en daar waar |Ψ|² een maximale waarde heeft, een piek.

Het feit dat het interferentiepatroon zelfs dan ontstaat wanneer de elektronen (of fotonen) één voor één door de spleten gaan, maakt duidelijk dat het patroon niet het gevolg is van interactie tussen het ene elektron en het andere. Dat hoeft ons ook niet te verbazen, want zoals we weten is een elektron niet alleen maar een deeltje. Het elektron is zowel een golf als een deeltje en een golf kan ongetwijfeld door beide spleten tegelijk gaan.
Maar wat gebeurt er als we een van beide spleten afdekken, zodat we weten dat het elektron door de opengebleven spleet gaat en dan enige tijd later de andere spleet afdekken zodat het elektron nu door de spleet gaat die eerst was afgedekt? Het resultaat is dat er geen interferentiepatroon ontstaat. We zien nu achter elke spleet alleen maar een heldere vlek op het scherm. Deze uitkomst bevestigt ons eerdere idee: zijn beide spleten open, dan gaat elk elektron door beide spleten, als was het een golf en toch maakt elk elektron een klein vlekje op het scherm, als was het een deeltje.

Het gaat in deze uitleg om het volgende. Behandelen we elektronen (of andere materiedeeltjes) als golven, dan geeft Ψ de golfamplitude weer. Behandelen we elektronen als deeltjes, dan moeten we redeneren op basis van waarschijnlijkheden. Het kwadraat van de golffunctie |Ψ|², is de waarschijnlijkheid per eenheid van volume een gegeven elektron in een gegeven punt aan te treffen. Het is onmogelijk het traject door ruimte en tijd van één elektron precies te voorspellen of zelfs maar te volgen.
terug naar de Inhoud

42-3 De onbepaaldheidsrelatie van Heisenberg
Elk meting die we doen, gaat gepaard met een zekere mate van onnauwkeurigheid. Zo is het bijvoorbeeld onmogelijk om met absolute nauwkeurigheid de lengte van een tafel te meten. Wanneer onze meetlat een millimeterverdeling heeft, is de mogelijke meetfout in het resultaat ongeveer 0,5 mm. Naarmate we een nauwkeuriger meetinstrument gebruiken, worden onze uitkomsten steeds preciezer, maar hoe goed ons instrument ook mag zijn, het eindresultaat bevat altijd een mogelijke meetfout. We verwachten evenwel dat we de onnauwkeurigheid in het meetresultaat in principe willekeurig klein kunnen maken door met steeds nauwkeuriger instrumenten te meten.
Volgens de quantummechanica is er echter een onoverschrijdbare grens aan de nauwkeurigheid van bepaalde metingen en deze grens wordt niet bepaald door de kwaliteit van ons meetinstrument, maar wordt ons opgelegd door de natuur. De onbepaaldheid waarover we het hier hebben, is het gevolg van twee factoren, namelijk van het feit dat deeltjes tegelijk ook golfeigenschappen hebben (golfdeeltje-dualiteit) en van de onvermijdelijke interactie tussen het waargenomen systeem en het waarnemingsinstrument.
Het is onmogelijk aan een voorwerp een meting te doen zonder dit voorwerp op zijn minst een beetje te verstoren. Stel dat u in een volkomen donkere kamer een pingpongbal tracht te vinden. Op zoek naar de bal tast u in het donker rond, maar op het moment waarop u de bal tenslotte met uw vinger aanraakt, stoot u die weg. Wanneer we de plaats van een voorwerp bepalen, raken we die ongeacht of het een pingpongbal of een elektron betreft - altijd met iets anders aan, dat ons vertelt waar het voorwerp zich bevindt. Wie in een donkere kamer naar een pingpongbal zoekt, kan dat doen door met zijn hand voor zich uit te tasten, of door net zolang met een lantaarn rond te schijnen totdat hij het licht ziet dat door de bal gereflecteerd wordt. Zoekt u door met uw hand rond te tasten, dan vindt u de plaats van de bal op het moment waarop u die aanraakt.
Door de bal echter aan te raken, geeft u die onvermijdelijk een duwtje en daarmee een zekere impuls, en dat betekent dat u nu niet kunt weten wat de toekomstige plaats van de bal wordt. Hetzelfde zou ook gelden, zij het in veel mindere mate, indien u de bal met behulp van licht zou lokaliseren. Wil de bal 'zichtbaar' zijn, dan moet die een of meer fotonen weerkaatsen en de teruggekaatste fotonen moeten dan uw oog of een andere detector binnengaan. Wanneer een foton een voorwerp van normale omvang treft, wordt de beweging of de plaats van het voorwerp daar maar weinig door veranderd. Maar een foton dat een zeer klein voorwerp, zoals een elektron, treft, kan een groot deel van zijn impuls aan het elektron overdragen en daarmee de beweging en de plaats van het elektron op een onvoorspelbare manier wijzigen. De handeling waarmee we meten op welke plaats een voorwerp zich op een gegeven tijdstip bevindt, maakt onze kennis van de toekomstige plaats van het voorwerp dus onnauwkeurig.

We bekijken nu welke rol de golfdeeltje-dualiteit in deze kwestie speelt. Stelt u zich een gedachtenexperiment voor waarin we met hulp van fotonen de plaats van een voorwerp - bijvoorbeeld een elektron - willen bepalen. Zoals we in hoofdstuk 38 hebben gezien, is de nauwkeurigheid waarmee we voorwerpen kunnen zien, nooit groter dan de golflengte van het gebruikte licht. Willen we een nauwkeurige plaatsbepaling, dan moeten we licht gebruiken met een korte golflengte. Maar een korte golflengte komt overeen met een hoge frequentie en een hoge energie, want E = hf; hoe meer energie de fotonen hebben, des te meer impuls kunnen ze bij botsing aan het voorwerp overdragen.
Gebruiken we echter fotonen met een langere golflengte en dus een geringere energie, dan wordt de beweging van het voorwerp, wanneer het door de fotonen getroffen wordt, minder sterk beïnvloed. Maar de langere golflengte betekent een lager oplossend vermogen; daardoor kan nu de plaats van het voorwerp minder nauwkeurig bekend zijn. De handeling van het waarnemen geeft een aanzienlijke onbepaaldheid in hetzij de plaats, hetzij de impuls van het elektron en dit is de essentie van het onbepaaldheidsprincipe, dat voor het eerst in 1927 door Heisenberg werd geformuleerd.

Heisenberg stelde een wiskundige formulering op van de onbepaaldheidsrelatie. Deze relatie zegt ons dat het onmogelijk is gelijktijdig zowel de plaats als de impuls van een voorwerp nauwkeurig te meten. Hoe nauwkeuriger we de plaats meten, dus hoe kleiner Δ.x wordt, des te groter wordt de onbepaaldheid in de impuls, Δ.p. Meten we daarentegen de impuls heel precies, dan wordt de onbepaaldheid in de plaats heel groot. De onbepaaldheidsrelatie verbiedt echter niet de meting van één van beide grootheden. Zo is het bijvoorbeeld in principe mogelijk de plaats van een voorwerp nauwkeurig te meten. De impuls van het voorwerp zou dan echter volledig onbekend zijn. We zouden in dat geval weten waar het voorwerp zich op het gegeven tijdstip bevindt, maar niet weten waar het een ogenblik later is.

Een andere nuttige vorm van de onbepaaldheidsrelatie legt verband tussen energie en tijd. Er is een onbepaaldheid in de plaats van het te detecteren voorwerp. Het foton dat gebruikt wordt om het voorwerp te detecteren, verplaatst zich met een snelheid c en doet er een bepaalde tijd over om de afstand van die onbepaaldheid te doorlopen.
Er is een bepaalde onbepaaldheid voor wat betreft het tijdstip waarop het voorwerp volgens onze metingen op een gegeven plaats is. Daar het foton zijn energie E gedeeltelijk of geheel aan het voorwerp kan overdragen, is er ook een onbepaaldheid in de energie van het voorwerp. Deze vorm van het onbepaaldheidsprincipe zegt ons dat ook de energie van een voorwerp onbepaald kan zijn, of zelfs mogelijk niet behouden blijft.

In het bovenstaande bespraken we de plaats en de snelheid van het elektron als betrof het een deeltje. Het elektron is echter geen deeltje en vandaar ook het onbepaaldheidsprincipe; dat dit principe van kracht is, komt doordat het elektron - en materie in het algemeen - zowel golf- als deeltjeseigenschappen heeft. Het onbepaaldheidsprincipe zegt ons eigenlijk het volgende: wanneer we ons het elektron willen voorstellen als deeltje, kiezen we voor een vereenvoudigd gezichtspunt dat bepaalde beperkingen heeft:
- het is dan namelijk niet mogelijk gelijktijdig zowel de plaats als de snelheid te kennen en
- de energie kan voor een zekere tijdsduur onbepaald zijn, of niet behouden blijven.
Doordat h, de constante van Planck een erg klein getal is, zijn de onbepaaldheden die door het onbepaaldheidsprincipe geformuleerd worden op macroscopisch niveau gewoonlijk verwaarloosbaar klein. Op atomair niveau zijn die onbepaaldheden echter wel van betekenis en aangezien ook voorwerpen van gewone afmetingen uit atoomkernen en elektronen bestaan, is het onbepaaldheidsprincipe uiteindelijk ook van belang voor een goed begrip van de macroscopische natuur. Het waarschijnlijkheidskarakter van de quantummechanica komt misschien wel het duidelijkst tot uitdrukking in het onbepaaldheidsprincipe en daarom kiest men dit principe vaak als uitgangspunt van filosofische discussie.
terug naar de Inhoud

42-4 De filosofische implicaties: waarschijnlijkheid versus determinisme
Het klassieke Newtoniaanse wereldbeeld is deterministisch. Een van de uitgangspunten van dit wereldbeeld is dat we, gegeven de plaats en de snelheid van een voorwerp op een bepaald tijdstip, de toekomstige plaats van dat voorwerp kunnen voorspellen indien de krachten op het voorwerp bekend zijn. Als bijvoorbeeld een steen telkens onder dezelfde beginhoek en met dezelfde beginsnelheid wordt weggeworpen en de krachten op de steen telkens dezelfde zijn, zal de steen iedere keer dezelfde baan beschrijven. Zijn de krachten (zwaartekracht en eventueel luchtweerstand) bekend, dan kan de baan van de steen en dus ook de plaats waar de steen neerkomt, worden voorspeld. Dit mechanistische gezichtspunt impliceert dat de toekomstige ontwikkeling van het heelal (waarvan men veronderstelt dat het uit afzonderlijke lichamen bestaat) volledig gedetermineerd is.

Onder invloed van de quantummechanica onderging de klassieke deterministische opvatting van de fysische wereld een radicale verandering. Zoals we hebben gezien in de analyse van het dubbelspleetexperiment (par. 42-2), komen de elektronen - ook al hebben ze elk dezelfde voorgeschiedenis - niet allemaal op dezelfde plaats terecht. Volgens de quantummechanica bestaat er voor elk punt een bepaalde waarschijnlijkheid dat er in dat punt een elektron aankomt. Dit is een heel ander gezichtspunt dan de klassieke opvatting, want volgens die opvatting wordt de baan van een deeltje volledig vastgelegd door zijn beginpositie en beginsnelheid en door de krachten die het ondergaat.
Volgens de quantummechanica is het zelfs niet eens mogelijk gelijktijdig zowel de plaats als de snelheid van een voorwerp te kennen. Deze beperking wordt uitgedrukt door de onbepaaldheidsrelatie en is een gevolg van het feit dat 'deeltjes', zoals elektronen, niet eenvoudigweg deeltjes zijn; ze hebben namelijk ook golfeigenschappen. Het enige waartoe de quantummechanica ons in staat stelt is voor een verzameling punten de kans te berekenen dat bijvoorbeeld een elektron (indien voorgesteld als een deeltje) in een bepaald punt wordt waargenomen. De quantummechanica zegt dus dat onvoorspelbaarheid inherent is aan de natuur. (overeenkomend met de 'dynamisch systeemtheorie' (Freek))
Doordat materie een samenstelsel van atomen is, mogen we verwachten dat zelfs voorwerpen van gewone afmetingen zijn onderworpen aan toeval en waarschijnlijkheid en niet beantwoorden aan een strikt determinisme. Zo bestaat er een eindig kleine (maar zeer geringe) kans dat een steen, na te zijn weggegooid, niet volgens een paraboolbaan omlaagvalt, maar plotseling naar omhoog afbuigt.
Uit de quantummechanica volgt dat gewone voorwerpen zich met zeer hoge waarschijnlijkheid zo zullen gedragen als door de klassieke natuurwetten voorspeld wordt. Maar die voorspellingen zijn waarschijnlijkheden en geen zekerheden. Dat macroscopische voorwerpen zich met zeer grote waarschijnlijkheid zullen gedragen in overeenstemming met de klassieke natuurwetten, komt doordat het in zulke gevallen gaat om grote aantallen moleculen: wanneer in een statistische situatie grote aantallen objecten zijn betrokken, worden de afwijkingen van het gemiddelde verwaarloosbaar klein. De gemiddelde configuratie van grote aantallen moleculen voldoet dus met grote waarschijnlijkheid aan de 'onveranderlijke' wetten van de klasieke natuurkunde en zo ontstaat er een schijnbaar determinisme. Hebben we echter te maken met een klein aantal moleculen, dan zijn afwijkingen van de klassieke wetten gemakkelijk waar te nemen. We kunnen dus zeggen dat de quantummechanica geen exacte, deterministische wetten kent, maar wel op waarschijnlijkheid gebaseerde statistische wetten.

Men dient in te zien dat er een verschil bestaat tussen de waarschijnlijkheid die door de quantummechanica wordt beschreven en het begrip waarschijnlijkheid zoals dat in de negentiende eeuwse natuurkunde gebruikt werd om thermodynamica en het gedrag van gassen te begrijpen in termen van moleculen. De reden dat er in de thermodynamica gebruik wordt gemaakt van kansrekening en van het begrip waarschijnlijkheid is, dat het hier om zoveel moleculen gaat, dat we ze onmogelijk afzonderlijk kunnen volgen. Maar daarbij wordt er nog steeds vanuit gegaan dat de moleculen zich elk op een deterministische manier gedragen en zich dus verplaatsen en met elkaar in wisselwerking treden volgens de wetten van Newton. De waarschijnlijkheid die we in de quantummechanica tegenkomen, is van een heel andere aard; hier wordt waarschijnlijkheid gezien als inherent aan de natuur en niet als een beperking van ons vermogen berekeningen te maken.

Ofschoon een klein aantal natuurkundigen de deterministische opvatting van de natuur nog altijd niet heeft opgegeven en weigert de quantummechanica als een complete theorie te accepteren - een van die natuurkundigen was Einstein - wordt de quantummechanica en het waarschijnlijkheidskarakter van de natuur tegenwoordig door de meeste natuurkundigen aanvaard. De opvatting die we hier als de algemeen geaccepteerde opvatting hebben gepresenteerd, wordt - ter ere van de woonplaats van Niels Bohr - de 'Kopenhaagse interpretatie' van de quantummechanica genoemd, omdat de theorie voor een groot deel in Kopenhagen werd ontwikkeld, in discussies tussen Bohr en andere vooraanstaande natuurkundigen.

Omdat elektronen niet eenvoudigweg deeltjes zijn, is het onjuist ons voor te stellen dat elektronen een welomschreven baan in ruimte en tijd volgen. Beschrijvingen van materie in tijd en ruimte zijn dus mogelijk niet helemaal correct, een diepe en verrijkende conclusie die tot levendige filosofische discussies heeft geleid. De belangrijkste en meeste invloedrijke filosoof van de quantummechanica was misschien wel Bohr. Bohr verdedigde het standpunt dat het onmogelijk is een ruimte-tijd beschrijving te geven van feitelijke atomen en elektronen. Wanneer we echter een beschrijving moeten geven van experimenten met atomen of elektronen, ontkomen we er niet aan dat te doen in termen van ruimte en tijd, en gebruik te maken van nog andere begrippen die ons uit de gewone ervaring vertrouwd zijn, zoals de begrippen golf en deeltje. Onze beschrijving van experimenten moet ons er echter niet toe verleiden te gaan geloven dat atomen of elektronen zelf werkelijk als deeltjes in ruimte en tijd bestaan. Dit onderscheid tussen onze interpretatie van experimenten en wat 'werkelijk' in de natuur plaatsvindt, is van cruciaal belang.
terug naar de Inhoud

42-5 De tijdonafhankelijke vorm van de Schrödingervergelijking
Om in staat te zijn fysische systemen met behulp van quantummechanica kwantitatief te beschrijven, moeten we de golffunctie Ψ kunnen berekenen. Zoals in par. 42-2 werd beschreven, is de fundamentele vergelijking (in het niet relativistische gebied) voor berekening van Ψ de vergelijking van Schrödinger. We kunnen de vergelijking van Schrödinger echter niet afleiden uit nog fundamentelere principes, zoals het ook niet mogelijk is de tweede wet van Newton af te leiden. De vergelijking F = ma werd door Newton uitgevonden als beschrijving van het verband tussen de beweging van een lichaam en de netto toegepaste kracht.
Zoals we in de hoofdstukken over mechanica hebben gezien, voldoet de tweede wet van Newton buitengewoon goed: in de klassieke natuurkunde kan met deze wet als uitgangspunt een brede verscheidenheid van vraagstukken analytisch worden opgelost en de oplossingen die op die manier verkregen worden, stemmen volledig overeen met de resultaten van proeven. Elke fundamentele vergelijking ontleent haar geldigheid aan de overeenstemming met experimenten en dat geldt ook voor de vergelijking van Schrödinger: deze vergelijking is een fundamentele vergelijking van de quantummechanica en moest dus net als de tweede wet van Newton worden uitgevonden - en vervolgens in experimenten worden getest, een test die de vergelijking van Schrödinger volledig heeft doorstaan.
terug naar de Inhoud

42-7 Vrije deeltjes - Vlakke golven en golfpakketjes
Een vrij deeltje is een deeltje dat aan geen enkele kracht is onderworpen en we mogen de potentiële energie van zo'n deeltje nul stellen. In par. 42-5 speelde het begrip 'vrij deeltje' een rol in onze argumentatie voor de vergelijking van Schrödinger, maar nu zijn we geïnteresseerd in het vrije deeltje zelf en wordt er van de vergelijking van Schrödinger uitgegaan. Als de potentiële energie U(x) gelijk is aan 0, ziet de tijdsonafhankelijke Schrödingervergelijking er als volgt uit:

d²ψ/dx² + 2mE/h² . ψ = 0

Deze vergelijking komt ons bekend voor, want we zijn zo'n vergelijking al eerder tegengekomen in hoofdstuk 15, toen we de enkelvoudige harmonische oscillator bespraken. Een vrij deeltje met impuls p en energie E kunnen we weergegeven door een vlakke golf (a) die sinusoïdaal varieert.
Als we een deeltje willen beschrijven waarvan de plaats binnen nauwe grenzen bekend is - dat wil zeggen, een deeltje waarvan we weten dat het zich binnen een klein gebied in de ruimte bevindt - kunnen we gebruik maken van het begrip golfpakketje (b). Als voorbeeld toont de tekening een golfpakketje met een breedte Δ.x; het deeltje is hoogst waarschijnlijk in dit deel van de ruimte aan te treffen. Een binnen nauwe grenzen gelokaliseerd deeltje dat zich door de ruimte verplaatst kan worden weergegeven door een verschuivend golfpakketje.

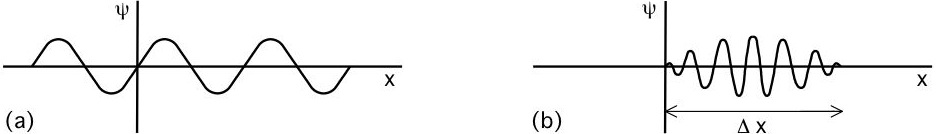Een golfpakketje kan wiskundig worden voorgesteld als de som van een groot aantal vlakke golven (sinusgolven) met elk een iets andere golflengte. Dat dit inderdaad mogelijk is, kunt u inzien door in Hoofdstuk 17 naar figuur 17-7 te kijken. In die figuur werden twee dicht bijeen gelegen frequenties gecombineerd om het ontstaan van zwevingen uit te leggen en daarbij vonden we dat de som van twee sinusgolven de vorm heeft van een reeks golfpakketjes. Tellen we bij dit patroon nog meer golven op met andere dicht bij elkaar gelegen frequenties, dan kunnen we op een na alle golfpakketjes elimineren en ontstaat het beeld van de tekening.
Een golfpakketje bestaat dus uit golven met een reeks van golflengten en daarom heeft zo'n pakket niet één bepaalde impuls p = h/λ, maar een reeks van impulswaarden. Dit stemt natuurlijk overeen met de onbepaaldheidsrelaties: doordat we Δ.x heel klein hebben gemaakt, heeft de impuls geen welomschreven waarde, zodat Δ.p niet nul kan zijn. We kunnen dus zeggen dat ons deeltje een reeks van impulswaarden heeft en dat er een onbepaaldheid Δ.p in de waarde van de impuls is. Er kan gemakkelijk worden aangetoond dat zelfs in deze eenvoudige situatie Δ.p = h/Δ.x, in overeenstemming met de onbepaaldheidsrelaties.
terug naar de Inhoud

42-8 Een deeltje in een potentiaalput
De vergelijking van Schrödinger kan alleen voor enkele speciale vormen van de potentiële-energiefunctie U, analytisch worden opgelost. We bekijken hier twee eenvoudige gevallen die misschien niet erg realistisch lijken, maar die eenvoudige oplossingen hebben waarmee we, door ze als benaderingen van de realiteit op te vatten, allerlei verschijnselen kunnen verklaren.

In het eerste geval nemen we aan dat een deeltje met massa m is opgesloten in een eendimensionale rechthoekige potentiaalput met oneindige, hoge wanden en een breedte L. De beschreven situatie zou bijvoorbeeld dienst kunnen doen als een zeer ruw model voor een elektron in een metaal. Het deeltje is opgesloten in de potentiaalput en maakt volmaakt elastische botsingen met de wanden. De potentiële energiefunctie voor deze situatie is weergegeven in de tekening en wordt omschreven als een oneindig diepe potentiaalput. De potentiële-energiefunctie, U(x), kan in dit geval worden beschreven met de tijdsonafhankelijke vergelijking van Schrödinger:
ψ(x) = A sin kx + B cos kx

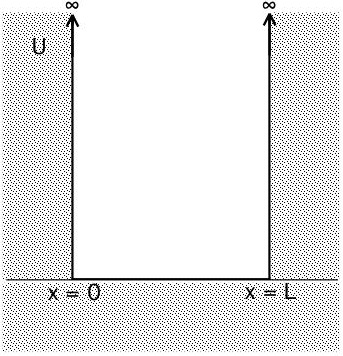Buiten de potentiaalput is U(x) = ∞, zodat ψ(x) (tijdsonafhankelijk) daar nul moet zijn. We hebben dus alleen te maken met de golffunctie binnen de potentiaalput en moeten voor deze golffunctie nu de constanten A en B (in de formule) bepalen en nagaan welke beperkingen er gelden voor de waarde van k en daarmee voor de energie E.

We hebben in het voorgaande met nadruk gesteld dat de golffunctie continu moet zijn. Gegeven dat buiten de potentiaalput ψ(x) = 0, moet de golffunctie ook nul zijn in x = 0 en x = L. De energie van een deeltje dat is opgesloten in een oneindig diepe potentiaalput kan alleen daarbinnen bepaalde waarden hebben en is gequantiseerd.
Voor de laatste energie, de grondtoestand geldt n = 1 en de energie bedraagt dan:
E₁ = h²/8mL²
Het positieve getal n noemen we het quantumgetal van de toestand. De vergelijking van Schrödinger geeft aan dat de laagste energie E₁ niet gelijk kan zijn aan nul, wat betekent dat het deeltje in de potentiaalput nooit in rust kan verkeren. Deze conclusie staat haaks op de klassieke opvatting, waarin wordt aangenomen dat de energie van een deeltje nul kan zijn (E = 0). E₁ wordt de nulpuntsenergie genoemd. Een van de implicaties van dit resultaat is dat volgens de quantummechanica deeltjes in een potentiaalput zelfs bij het absolute nulpunt (0°K) niet in rust verkeren, maar een nulpuntsenergie bezitten (dit is de oorzaak van het zogenoemde 'nulpunt-energieveld'). Doordat zij gequantiseerd zijn, is hun E gelijk aan E₁, 2E, 3E... nE enz. Daarbij is n het kwantumgetal van de energietoestand.

Verder valt op te merken dat in de grondtoestand de energie E₁ en de impuls p = hk = hπ/L omgekeerd evenredig zijn aan de breedte van de potentiaalput: hoe kleiner de breedte L, des te groter is de impuls p en de energie. We kunnen dit beschouwen als een direct gevolg van het onbepaaldheidsprincipe. Dat betekent dat in hoe kleiner gebiedje een deeltje wordt opgesloten, des te hoger de energie van dat deeltje zal zijn.

De amplitude A is voor alle quantumgetallen gelijk. In de tekening (a) zijn de golffuncties voor n = 1, 2, 3 afgebeeld. Ze zien er precies zo uit als staande golven in een snaar en dat is begrijpelijk, want de oplossingen die we voor de golffunctie ψ vonden zijn dezelfde als die voor staande golven in een snaar.

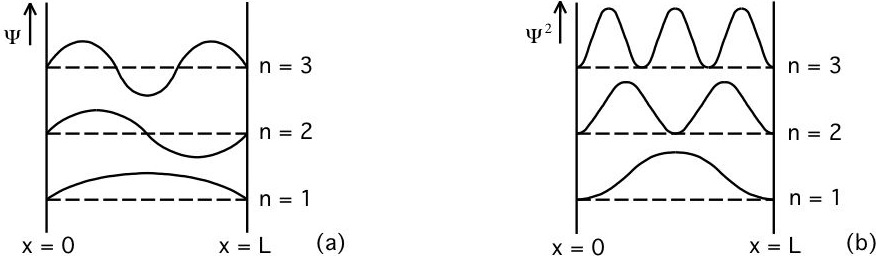In (b) is voor de toestanden waarvoor in (a) de golffunctie ψ is getekend (n = 1, 2, 3) de waarschijnlijkheidsdichtheid |ψ|², weergegeven. We zien daardoor dat de kans het deeltje aan te treffen niet in alle punten even groot is. Als het elektron in de grondtoestand verkeert, is de kans bijvoorbeeld veel groter dat het in de buurt van het midden van de potentiaalput dan nabij de wanden wordt aangetroffen.
Deze conclusie verschilt duidelijk van hetgeen de klassieke natuurkunde hier voorspelt, want volgens deze zou de waarschijnlijkheidsdichtheid overal in de potentiaalput gelijk zijn en zou de kans het deeltje aan te treffen in elk punt binnen de potentiaalput even groot zijn. De quantummechanische waarschijnlijkheidsdichtheden voor de hogere toestanden zijn ingewikkelder van vorm, met niet alleen gebieden van lage waarschijnlijkheid nabij de randen, maar ook op regelmatige afstanden daartussen (b).

We bekijken nu een deeltje dat zich bevindt in een potentiaalput waarvan de wanden niet oneindig hoog zijn. Dat wil zeggen, de potentiële energie is buiten de put nu niet oneindig, maar neemt daar toe tot een of andere eindige waarde, U = U₀ (zie tekening (a)). Deze situatie, die een eindig diepe potentiaalput genoemd wordt, kan dienen als ruw model voor bijvoorbeeld een neutron in een atoomkern.
De eindig diepe put blijkt, wanneer we die vergelijken met de oneindig diepe put, enkele belangrijke nieuwe eigenschappen te hebben. We verdelen de put in drie gebieden, I, II, III op de manier die is aangegeven (a). In het binnen de put gelegen gebied II geldt dezelfde vergelijking van Schrödinger als in het voorgaande (U = 0), ofschoon de randvoorwaarden nu anders zijn.

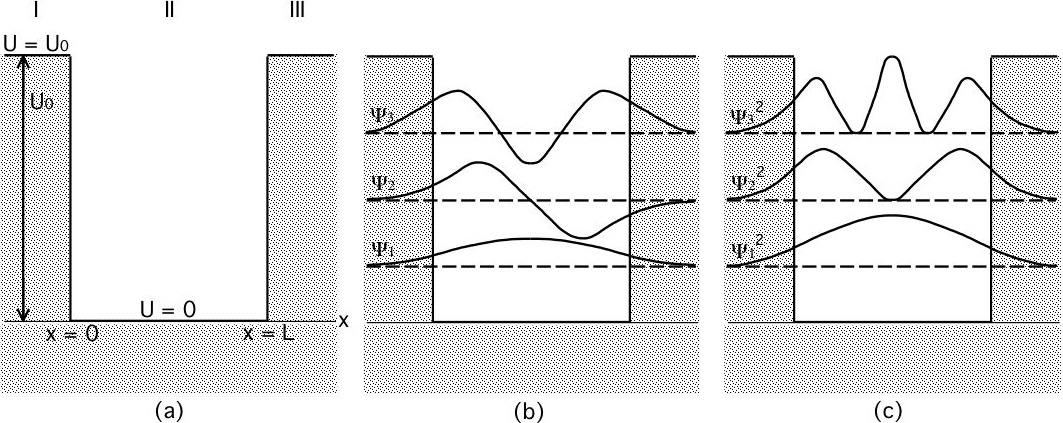We geven hier geen details van de wiskundige afleiding maar zullen alleen enkele uitkomsten bespreken.
Tekening (b) toont de golffunctie ψ voor de drie laagste energietoestanden die mogelijk zijn en (c) de corresponderende waarschijnlijkheidsdichtheidfuncties |ψ|². We zien in deze figuur dat de golffuncties bij de randen van de put een vloeiend verloop hebben. Binnen de potentiaalput heeft ψ de vorm van een sinusoïdale golf, die in het geval van de grondtoestand uit minder dan een halve golflengte bestaat.
Vergelijk dit met de oneindig diepe potentiaalput; in dat geval is de golffunctie voor de grondtoestand (n = 1) precies een halve golflengte, waardoor λ = 2L. Voor onze eindig diepe put geldt echter dat λ > 2L. De impuls (p = h/λ) en daardoor ook de energie van een deeltje in de grondtoestand (n = 1) is voor een eindig diepe put dus kleiner dan voor een oneindig diepe put met dezelfde breedte L.

Buiten de eindig diepe put zien we de golffunctie ter weerszijden van beide wanden exponentieel afnemen. Dat ψ voorbij de wanden niet nul is, betekent dat we het deeltje soms voorbij de wanden kunnen aantreffen! Deze conclusie is volledig in tegenspraak met wat de klassieke natuurkunde hier beweert. Buiten de put zou het deeltje een potentiële energie hebben die groter is dan zijn totale energie: U₀ > E en dat is in tegenspraak met de wet van behoud van energie. Tekening (c) laat echter duidelijk zien dat het deeltje enige tijd buiten de put kan verblijven, dus in het gebied waar U₀ > E; hoewel het meestal niet ver in dit klassiek verboden gebied doordringt, want voor elke wand geldt dat |ψ|² voorbij de wand exponentieel afneemt met de afstand.
Dat een deeltje kan doordringen in een gebied dat volgens de klassieke natuurkunde verboden terrein is, is een hoogst belangrijke implicatie van de quantummechanica. Maar hoe is zoiets mogelijk? Hoe kunnen we accepteren dat er niet wordt voldaan aan de wet van behoud van energie? Het onbepaaldheidsprincipe zegt echter dat ook energie een zekere onbepaaldheid bevat en dat de wet van behoud van energie gedurende een zeer korte tijd met een waarde Δ.E kan worden overschreden!
terug naar de Inhoud

42-9 Tunnelen door een barrière
In par. 42-8 hebben we gezien dat een deeltje, zoals een elektron, volgens de quantummechanica door een barrière kan doordringen in een gebied dat volgens de klassieke mechanica verboden terrein is. Dit verschijnsel kent een aantal belangrijke toepassingen, waarin de barrière die moet worden doordrongen, meestal heel dun is.
We bekijken een deeltje met een massa m en energie E, dat zich in de vrije ruimte (waarin de potentiële energie U = 0, zodat E = KE) langs de x-as naar rechts verplaatst, zie tekening. Het deeltje ontmoet op zijn weg een smalle potentiaalbarrière met een hoogte U₀ (in energie eenheden) die groter is dan E en een breedte L (afstandseenheden) heeft. Daar E < U₀ zouden we op grond van de klassieke natuurkunde verwachten dat het deeltje niet door de barrière heen kan dringen en dus gewoon weerkaatst wordt en in omgekeerde richting teruggaat. Dat is inderdaad wat er gebeurt met macroscopische voorwerpen.
De quantummechanica voorspelt echter dat de kans het deeltje aan de andere kant van de barrière aan te treffen niet gelijk is aan nul. Hoe dit mogelijk is, zien we in de tekening waarin de golffunctie ψ is weergegeven. Het naderende deeltje heeft een sinusoïdale golffunctie. Binnen de barrière is de oplossing voor de vergelijking van Schrödinger een afnemende exponentiële functie net als voor de eindig diepe potentiaalput van par. 42-8. Op de plaats waar de barrière eindigt (in x = L) is de exponentiële functie echter nog niet tot nul afgenomen en voorbij de barrière (dus voor x > L) is de golffunctie weer sinusoïdaal, want in dit gebied is U = 0 en is E = KE > 0. Hoewel de sinusoïdale golf voorbij de barrière een sterk afgenomen amplitude heeft, is |ψ|² hier ongelijk aan nul en we zien dus dat de kans dat het deeltje door de barrière dringt, groter is dan nul.
We noemen dit proces het tunnelen door een barrière, ofwel het 'tunneleffect'. Het deeltje kan niet worden waargenomen wanneer het zich in de barrière bevindt (want dat zou in strijd zijn met de wet van behoud van energie), maar we kunnen het wel detecteren nadat het door de barrière is heengedrongen.

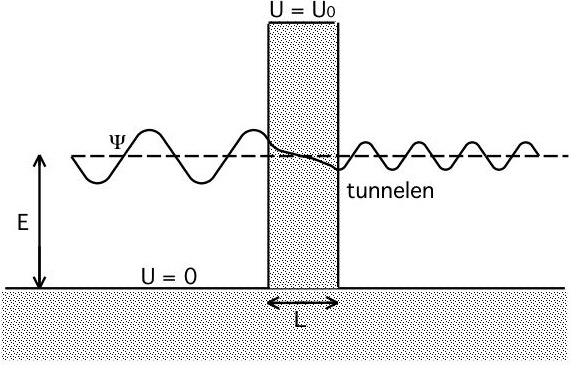Tunnelen is een gevolg van de golfeigenschappen van materiedeeltjes en doet zich ook voor met klassieke golven. Zo zagen we in par. 35-6 dat licht dat zich voortplant door glas voor 100 procent wordt teruggekaatst wanneer het onder een hoek groter dan de kritische hoek een grensvlak met lucht treft. Toen we dit verschijnsel - totale inwendige reflectie - beschreven, gingen we uit van de geometrische optica. De golftheorie voorspelt echter dat golven in werkelijkheid over een afstand van enkele golflengten tot voorbij het grensvlak in de lucht zullen doordringen - bijna alsof ze het grensvlak een klein stukje voorbij moeten gaan om vast te stellen dat er zich aan de andere kant lucht bevindt en dat ze dus volledig moeten reflecteren. Als een tweede stuk glas heel dicht bij het eerste wordt gebracht, kan er inderdaad een doorgelaten golf worden waargenomen die door tunnelen de luchtspleet is overgestoken.
U kunt dit zelf waarnemen door onder een zodanige hoek in een glas water omlaag te kijken, dat het licht dat uw oog binnenkomt totale inwendige reflectie heeft ondergaan tegen het buitenoppervlak van het glas (het glas ziet er dan zilverachtig uit). Drukt u nu een vochtige vingertop tegen het glas, dan ziet u een spiraalvormige vingerafdruk, doordat de ribbeltjes van uw vinger daar waar ze het glas raken de totale inwendige reflectie aan het buitenoppervlak van het glas verstoren; op die plaatsen ziet u dus licht dat door het glasoppervlak is heengedrongen en tegen de ribbeltjes op uw vinger is gereflecteerd.

Hoewel het tunneleffect ook optreedt met klassieke golven, is het nieuwe van de quantummechanica dat ook materiedeeltjes golfeigenschappen blijken te hebben en daardoor kunnen tunnelen. Het tunneleffect heeft diverse nuttige technische toepassingen (zoals de tunneleffectmicroscoop) en maakt het mogelijk een verklaring te geven voor een aantal belangrijke verschijnselen, waarvan we er nu enkele in het kort bespreken.

Sommige atoomkernen ondergaan radioactief verval door emissie van een alfadeeltje, dat bestaat uit twee protonen en twee neutronen. De protonen en neutronen in een atoomkern zijn - op hun plaats binnen de kern - in heftige beweging; soms komen er twee neutronen en twee protonen bij elkaar, zodat er binnen de kern een nieuwe stabiele eenheid, een 'alfadeeltje', ontstaat. Het potentiële energiediagram voor het alfadeeltje in een atoomkern die alfaverval vertoont, komt overeen met de tekening.

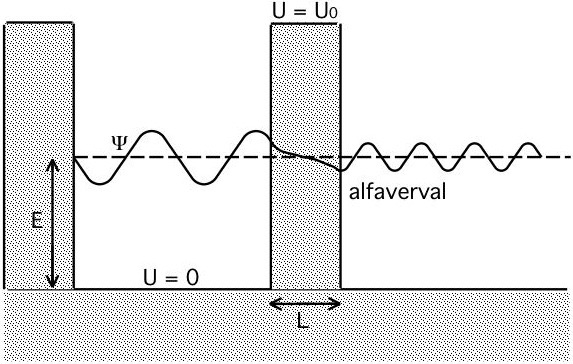De rechthoekige potentiaalput geeft de aantrekkende kernkracht weer die de kern bijeen houdt en daaraan toegevoegd is de potentiële energie van de afstotende coulombkracht tussen het positieve alfadeeltje en de resterende positief geladen kern. De potentiaalbarrière die zo ontstaat, wordt de coulombbarrière genoemd. De energie van de golffunctie voor het tunnelende deeltje moet groter zijn dan nul (anders zou de barrière een oneindige breedte hebben en zou tunnelen niet mogelijk zijn), maar moet kleiner zijn dan de hoogte van de barrière.
Zou de energie van het alfadeeltje hoger zijn dan de barrière, dan zou het deeltje altijd vrij zijn en zou de oorspronkelijke kern niet bestaan. De barrière zorgt er dus voor dat de atoomkern bijeen wordt gehouden, maar zo nu en dan kan een kern van dit type vervallen, doordat er een alfadeeltje naar buiten tunnelt.
terug naar de Inhoud

Samenvatting
In 1925 werkten Schrödinger en Heisenberg elk afzonderlijk een nieuwe theorie uit, de quantummechanica, die thans geldt als de fundamentele theorie voor het atomaire en subatomaire domein. De quantummechanica is een statistische en geen deterministische theorie.
Een van de belangrijkste relaties in de quantummechanica is de onbepaaldheidsrelatie van Heisenberg. Het onbepaaldheidsprincipe is een gevolg van
- de golfdeeltje-dualiteit en
- de onvermijdelijke interactie tussen waargenomen object en waarnemer.
Het onbepaaldheidsprincipe kan op verschillende manieren worden geformuleerd. Een van die formuleringen zegt dat het onmogelijk is gelijktijdig zowel de plaats x als de impuls p van een voorwerp nauwkeurig te meten.
Een andere formulering van het onbepaaldheidsprincipe zegt dat de energie onbepaald kan zijn of mogelijk niet behouden blijft met een waarde Δ.E gedurende een zeer korte tijd.

Een deeltje zoals een elektron wordt weergegeven door een golffunctie, ψ. Het kwadraat van de golffunctie, |ψ|² in een willekeurig punt in de ruimte geeft de waarschijnlijkheid het deeltje in dat punt aan te treffen. De golffunctie moet genormaliseerd zijn en daarmee bedoelen we dat ψ².Δ.V over de hele ruimte genomen gelijk aan 1 moet zijn, want het deeltje moet altijd ergens zijn aan te treffen. In de niet relativistische golfmechanica voldoet ψ aan de vergelijking van Schrödinger:
- h²/2m . d²ψ/dx² + Uψ = Eψ
die hier is geschreven in zijn eendimensionale, tijdsonafhankelijke vorm; daarin is U de potentiële energie als functie van plaats en E de totale energie van het deeltje.
Een vrij deeltje dat aan geen enkele kracht is onderworpen, heeft een sinusoïdale golffunctie: ψ = A sin kx + B cos kx, waarin k = p/h en waarin p de impuls van het deeltje is. Zo'n golf waarvan de impuls vastligt, strekt zich als een vlakke golf oneindig ver in de ruimte uit. Een golfpakketje dat zich op een vaste plaats in de ruimte bevindt, is een superpositie van sinusoïdale golven die elk een andere impuls hebben.

Voor een deeltje dat in een oneindig diepe potentiaalput is opgesloten, vinden we met de vergelijking van Schrödinger als oplossingen binnen de put golffuncties ψ = A sin kL; de energie is gequantiseerd. In een eindig diepe potentiaalput strekt de golffunctie zich uit tot in het gebied dat volgens de klassieke natuurkunde verboden terrein is en waar de totale energie kleiner is dan de potentiële energie. Dat dit mogelijk is, is in overeenstemming met het onbepaaldheidsprincipe. In deze gebieden zijn de oplossingen van de vergelijking van Schrödinger afnemende exponentiële functies.
Doordat quantummechanische deeltjes in zulke klassiek verboden gebieden kunnen doordringen, zijn ze in staat door dunne barrières te tunnelen, ook al is de potentiële energie in de barrière groter dan de totale energie van het deeltje.
terug naar de Inhoud

Hoofdstuk 43 - De quantummechanica van atomen

Inleiding
Aan het begin van hoofdstuk 42 bespraken we de beperkingen van de atoomtheorie van Bohr en lieten daarmee zien waarom er behoefte bestond aan een nieuwe theorie. Kort samengevat kwam het neer op het volgende: de theorie van Bohr voorspelde met veel succes de golflengte van het licht dat wordt uitgezonden en geabsorbeerd door het waterstofatoom, maar gaf geen correcte voorspelingen voor de absorptie en emissiespectra van ingewikkelder atomen. De theorie gaf ook geen verklaring voor de fijnstructuur, het verschijnsel dat afzonderlijke emissielijnen in feite uit twee of meer lijnen bestaan die heel dicht bij elkaar liggen. Daar kwam nog bij dat Bohrs theorie een ongemakkelijke combinatie was van klassieke en quantumideeën. Al deze problemen verdwenen met de komst van de quantummechnica in 1925 en 1926. In dit hoofdstuk bespreken we de quantummechanische theorie van de atoomstructuur, een theorie die veel completer is dan de theorie van Bohr.
terug naar de Inhoud

43-1 Het atoom volgens de quantummechanica
Bepaalde facetten van de theorie van Bohr zoals de stelling dat elektronen en atomen uitsluitend voorkomen in discrete toestanden die elk één bepaalde energie hebben en dat een elektron dat van de ene toestand naar de andere overgaat een lichtfoton uitzendt (of absorbeert) bleven in de quantummechanica gehandhaafd (of liever werden opnieuw bevestigd). De quantummechanica reikt echter veel dieper dan de theorie van Bohr en heeft ons een heel ander beeld van het atoom gegeven.

Volgens de quantummechanica volgen elektronen - anders dan in Bohrs theorie werd aangenomen - geen welomschreven banen. Volgens de quantummechanica is het elektron vanwege zijn golfkarakter als een wolk van negatieve lading over de ruimte uitgespreid. De grootte en vorm van de elektronenwolk kan voor een gegeven toestand van een atoom ook worden berekend. De vergelijking van Schrödinger geeft als oplossing voor het elektron in een waterstofatoom dat in de grondtoestand verkeert (we komen hier in §43-3 nog uitvoerig op terug):

ψ(r) = √ 1/π r 3₀³ . e^-r/r₀ (Schrödingervergelijking voor de golffunctie ψ)

In deze vergelijking is ψ(r) de golffunctie als functie van plaats (niet van tijd) en deze functie hangt alleen af van de radiale afstand (r) tot het middelpunt en niet van de hoeken θ of φ (De waarde van de constante r₀ is toevallig gelijk aan de eerste Bohr-straal.) De elektronenwolk voor de grondtoestand van waterstof heeft een waarschijnlijkheidsdichtheid |ψ|² en is dus, zoals afgebeeld in figuur 43-1 bolsymmetrisch.

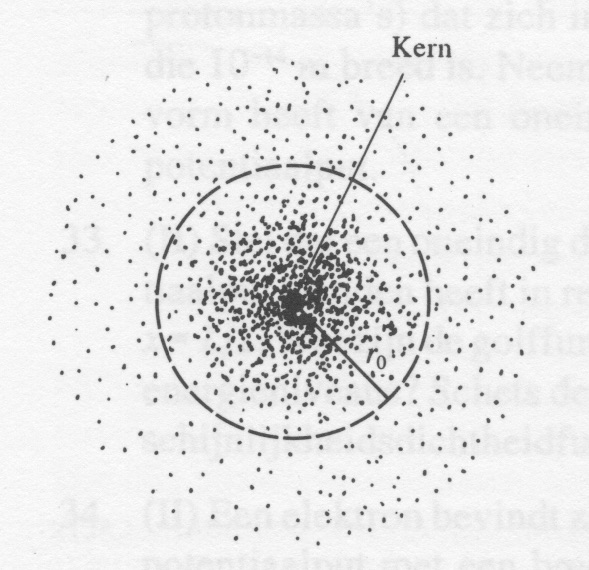De elektronenwolk geeft ruwweg de grootte van een atoom maar net zoals een regenwolk vaak geen scherp gedefinieerde grens heeft, hebben ook atomen geen nauwkeurige grens of welomschreven grootte. (Later in dit hoofdstuk zal nog blijken dat niet alle elektronenwolken bolvormig zijn.)

De boven gegeven vergelijking laat zien dat ψ(r) voor grote r weliswaar uiterst klein wordt, maar in geen enkel gebied van eindige omvang gelijk is aan nul. Volgens de quantummechanica bestaat een atoom dus niet overwegend uit lege ruimte. Uit het feit dat ψ→0 alleen als r→∞, volgt dat er in het heelal geen werkelijk lege ruimte voorkomt.

Wanneer we de elektronenwolk fysisch willen interpreteren, kunnen we uitgaan van hetzij het deeltjes-, hetzij het golfmodel. Bedenk dat we met een deeltje iets bedoelen dat in de ruimte gelokaliseerd kan worden - een deeltje bevindt zich op elk tijdstip op een precies te definiëren plaats. Een golf daarentegen is over de ruimte uitgespreid. De elektronenwolk die over de ruimte verdeeld is op de manier die is aangegeven in figuur 43-1, kunnen we beschouwen als een gevolg van het golfkarakter van elektronen. We kunnen een elektronenwolk echter ook opvatten als de waarschijnlijkheidsverdeling voor een deeltje.

Zoals we hebben gezien in §42-3, kan niet worden voorspeld welk traject het elektron zal volgen. Nadat we de plaats van een elektron hebben bepaald, kunnen we niet exact voorspellen waar het zich op een later tijdstip zal bevinden. We kunnen alleen maar berekenen wat in elk punt de waarschijnlijkheid is dat we het elektron in het betreffende punt zullen aantreffen. Zouden we de plaats van het elektron achtereenvolgens 500 keer bepalen (waarbij we het elektron dan telkens als deeltje opvatten), dan zou het elektron het meest worden aangetroffen in punten die in figuur 43-1 in het donkere gebied liggen, namelijk daar waar de waarschijnlijkheid het grootst is. Slechts zo nu en dan zou het elektron worden aangetroffen in plaatsen waar de waarschijnlijkheid laag is.
terug naar de Inhoud

43-2 Het waterstofatoom: de Schrödingervergelijking en quantumgetallen

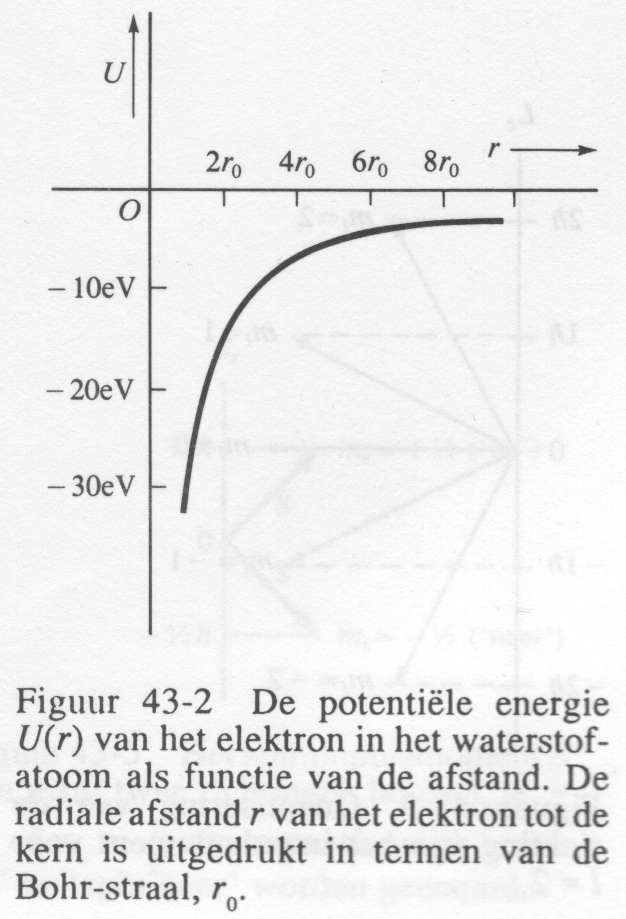Het waterstofatoom is van alle atomen het eenvoudigst en bestaat uit één elektron met een lading -e, dat zich verplaatst rond een centrale kern met één proton dat een lading +e heeft. We beginnen onze bespreking van de atoomstructuur daarom met waterstof.
In de vergelijking van Schrödinger (zie vergelijking 42-5) staat een term voor de potentiële energie. In het geval van het waterstofatoom (H) is de potentiële energie een gevolg van de coulombkracht tussen elektron en proton:

U = - 1/4 π ε₀ . e²/r

waarin r de radiale afstand tussen het proton (r = 0) en het elektron is; zie figuur 43-2.

terug naar de Inhoud

terug naar het literatuuroverzicht

terug naar Zo boven, zo beneden

^