Penrose-betegelingen in Middeleeuwse islamitische mozaïeken
Noorderlicht, 04-04-2007Islamitische mozaïeken bevatten soms bijzondere patronen, die lijken op de beroemde Penrose-betegelingen. Dat hebben twee Amerikaanse fysici vastgesteld. In Science verscheen vorige week een artikel van Peter Lu, natuurkundestudent uit Harvard en Paul Steinhardt, hoogleraar in Princeton. Ze hebben ontdekt dat in bepaalde islamitische mozaïeken bijzondere patronen zitten, die lijken op de beroemde Penrose-betegelingen (de hoeken daarvan zijn 36° en 72°, de hoeken van de gulden driehoek, waarvan er vijf het pentagon vormen).
Penrose-betegelingen
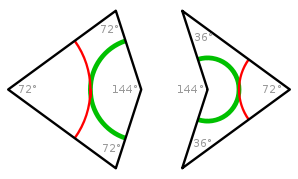Een Penrose-betegeling is een vlakvulling die aan speciale eigenschappen voldoet. Zo'n betegeling kun je maken met de volgende tegels, die ook wel vlieger en pijl genoemd worden:Deze tegels kunnen aan elkaar worden gelegd en het hele vlak opvullen. Je mag ze echter niet op elke willekeurige manier aan elkaar leggen: als twee zijden aan elkaar liggen, moeten de rode en groene lijnen aan elkaar passen.
Maar wat is er nou zo bijzonder aan een Penrose-betegeling? Je kunt het vlak toch ook opvullen met alleen vierkantjes of driehoekjes, of met rechthoeken zodat er een baksteenpatroon ontstaat? Het verschil met deze eenvoudigere patronen is dat een Penrose-betegeling zichzelf nooit herhaalt: hij is niet-periodiek. Dat betekent dat je een Penrose-betegeling niet zódanig kunt verschuiven dat hij weer op zichzelf terecht komt.
Bij een baksteenpatroon kan dat wel: als je alles precies één baksteen naar rechts verschuift, is het patroon precies hetzelfde. Het bijzondere aan de vlieger en pijl van Penrose is dat alle vlakvullingen die je ermee kunt maken niet-periodiek zijn.Penrose-ster
Er zijn verschillende manieren om met de vlieger en pijl van Penrose het vlak te vullen. We laten hier zien hoe je het volgende stervormige patroon kunt maken, willekeurig groot, zodat je inderdaad kunt spreken van een 'vlakvulling'.
Nu kun je daar een nieuwe figuur van maken door gebruik te maken van een zogenaamde deflatie-regel. Je vult elke halve vlieger op met (halve) Penrose-tegeltjes op de manier als in het plaatje hiernaast. Elke halve pijl vervang je zoals in het plaatje hiernaast.
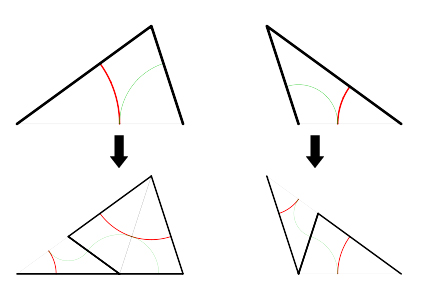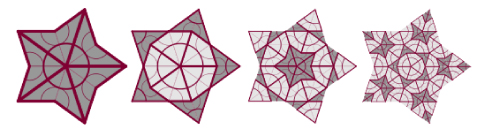
Het blijkt dat alle nieuwe halve vliegers en pijlen die je in de vergroting krijgt, weer precies grenzen aan een andere halve vlieger of pijl.Daardoor bestaat de nieuwe figuur inderdaad weer uit hele vliegers en pijlen in plaats van halve. Hieronder zie je wat je krijgt na één, twee en drie stappen.
Zo kun je verdergaan. Als je na elke stap alle tegeltjes vergroot totdat ze even groot zijn als de vlieger en pijl waarmee je begon, vind je een steeds grotere figuur van Penrose-tegeltjes, die je willekeurig ver kunt voortzetten.
De vlakvulling die je uiteindelijk wilt hebben vult het hele vlak, dus die kun je niet na een eindig aantal stapjes vinden: een figuur die uit een eindig aantal tegeltjes bestaat blijft uit eindig veel tegeltjes bestaan na het toepassen van de deflatie-regel. Je kunt ook een Penrose-betegeling maken door met andere figuurtjes van vliegers en pijlen te beginnen. Ook als je bijvoorbeeld met één pijl begint, of met één vlieger, vind je een Penrose-betegeling.Islamitische mozaïeken
Peter Lu en Paul Steinhardt hebben op verscheidene plaatsen Islamitische mozaïeken gevonden met patronen die heel erg lijken op Penrose-betegelingen. In de patronen die zij interessant vinden komen vijf tegels voor. De patronen zijn uiteindelijk nog iets ingewikkelder, omdat op deze vijf tegels ook nog lijnen getekend zijn. Maar aan de basis ligt duidelijk steeds een vlakvulling die vijf speciale tegels gebruikt.
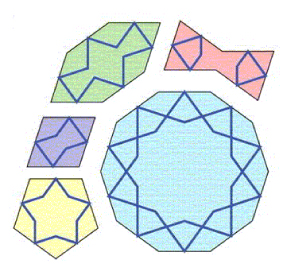Die vijf tegels zijn veelhoeken (een ruit, een 'strikje', een regelmatige tienhoek, een regelmatige vijfhoek en een niet-regelmatige zeshoek) en alle zijden van deze vijf tegels zijn precies even lang. Deze tegels kunnen opgevuld worden met tegels van dezelfde vorm, die allemaal met dezelfde factor verkleind zijn. (Bron: Science, zie onderaan)Je ziet dat aan de rand halve tegels gebruikt zijn. Maar als je een vlakvulling hebt van de vijf tegels, passen die halve tegels gelukkig weer precies aan de halve tegels aan de randen van de aangrenzende figuren, zodat je inderdaad een nieuwe vlakvulling krijgt die uit hele tegeltjes bestaat.
Opvullen van een grote tegel met de kleinere tegeltjes is net zo'n soort regel als de deflatie-regel in de Penrose-betegeling.
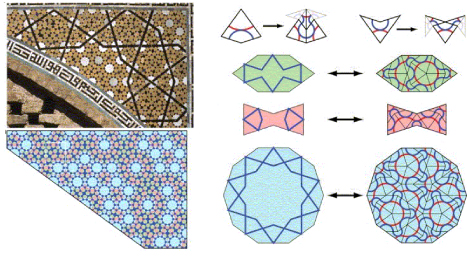Lu onderzocht een paar duizend foto's van patronen in moskeeën. Hoewel tienhoekige patronen vaker voorkwamen, waren de patronen bijna allemaal periodiek. Maar toen vond hij een foto van een mozaïek uit 1453 op een boog in het Darb-i Imam grafcomplex in Isfahan, Iran. Samen met Steinhardt kwam hij tot de conclusie dat dit mozaïek erg lijkt op een Penrose-betegeling. In dit patroon komt alleen de vijfhoek, de zeshoek en het strikje als tegel voor, zie de onderstaande figuur, links. Zoals je in onderstaande figuur, rechts, kunt zien, blijkt dat je die drie tegels kunt opvullen met de vliegers en pijlen van Penrose!
Op deze manier kun je het mozaïek opvullen met Penrose-tegels. Maar is het nu ook een Penrose-betegeling? Allereerst kloppen niet alle tegeltjes precies: op een paar plekken liggen de vliegers en pijlen aan elkaar op een manier die niet mag. Dat kan worden verholpen door een strikje en een zeshoek om te wisselen. Volgens Lu en Steinhardt zijn deze defecten oppervlakkig en kunnen ze best veroorzaakt zijn door de bouwers of een reparateur.
Een ander kenmerk van een Penrose-betegeling is echter dat hij het hele (oneindige) vlak vult. Als je een eindige betegeling hebt van Penrose-tegeltjes, dan kun je zonder uitbreidregel niet zeggen dat het een Penrose-betegeling is. Het mozaïek dat Lu en Steinhardt gevonden hebben, levert inderdaad een eindig stukje van een Penrose-betegeling op, maar ze geven geen regel om het gevonden mozaïek uit te breiden. Lu en Steinhardt merken wel op dat dat in principe kan.
Maragha
Lu en Steinhardt zijn niet de eersten met een dergelijke vondst. In 1992 concludeerde Emil Makovicky uit Denemarken al dat patronen op een graf in Maragha, Iran, ook aanleiding geven tot een Penrose-betegeling. Lu en Steinhardt zeggen echter dat ze serieuze problemen gevonden hebben in zijn technische reconstructie en zijn algehele conclusies.
Hoe dan ook: het mozaïek is mooi en levert na het opvullen van de tegels met Penrose-tegeltjes inderdaad een stukje van een Penrose-betegeling op. Dat geeft natuurlijk geen reden om te concluderen dat de Perzen in de middeleeuwen al wisten wat een Penrose-betegeling was, maar dat doen Lu en Steinhardt dan ook niet. Hun conclusie luidt, na het bestuderen van een heleboel mozaïeken, dat er rond het jaar 1200 een conceptuele doorbraak plaatsgevonden heeft bij het construeren ervan, waardoor dergelijke wiskundig ingewikkeldere patronen verzonnen konden worden.
Noorderlicht 22 februari 2007
Vijf tegels voor Allah
Islamitische architectuur vijf eeuwen voor op westerse meetkunde
Veel van de prachtige symmetrische patronen in de islamitische architectuur lijken gemaakt door een set van vijf verschillende basistegels als puzzelstukken tegen elkaar aan te leggen. Eén patroon is zelfs van een type dat westerse wiskundigen pas eind vorige eeuw ontdekten.
Waar een verbod al niet goed voor kan zijn: in de islamitische traditie mag je geen personen en wereldse zaken afbeelden, dus worden moskeeën en andere gebouwen in de islamitische wereld versierd met prachtige kalligrafie en abstracte geometrische patronen, 'girih' genoemd, vaak met veel vijf- en tienhoeken. De kunst van het maken van deze Escher-achtige versieringen bereikte sinds eind dertiende eeuw zelfs zulke hoogten, dat sommige van de gebruikte patronen door westerse wiskundigen pas in de jaren zeventig van de vorige eeuw werden doorgrond. Dat stellen Peter Lu en Paul Steinhardt, twee natuurkundigen van de Amerikaanse universiteiten Princeton en Harvard.
Geïnspireerd door een reis van Lu naar Oezbekistan bestudeerden ze duizenden foto's van geometrische patronen uit de islamitische kunst. Ze kwamen tot de conclusie dat architecten en handwerkslieden sets van drie, soms vijf verschillende tegels met vaste lijnpatronen gebruikten. Door die tegels tegen elkaar aan te leggen en als sjabloon te gebruiken zijn veel van de girih-patronen gemakkelijk te construeren. Tot nog toe werd aangenomen dat de patronen werden geconstrueerd met equivalenten van passer en lineaal, maar juist bij vijf- en tienhoeken is dat lastig. Grote patronen, die soms uit duizenden veelhoeken kunnen bestaan, zouden niet alleen erg veel werk opleveren, maar ook zouden foutjes bij het uitmeten zich langzamerhand opstapelen, zodat je op den duur niet uitkomt. Op één vijftiende-eeuwse perkamentrol, een soort handleiding voor architecten, zijn de girih-tegels zelfs met stippellijnen aangegeven.
Afgaand op de toenemende complexiteit van patronen rond 1200 na Christus, denken Lu en Steinhardt dat de tegels rond die tijd in zwang kwamen. Vanaf dat moment duiken in gebouwen ook patronen op die met passer en lineaal veel lastiger te maken zijn, en die met de vijf tegels juist makkelijk zijn. Tot nog toe zijn exemplaren van de tegels nog niet aangetroffen, maar met de toendertijd bekende wiskunde waren ze gemakkelijk te maken, stellen de onderzoekers. Lijnen op de tegels sluiten altijd mooi recht aan op lijnen van naburige tegels, en alle hoeken zijn veelvouden van 36 graden, een tiende van de volledige cirkel. Dat verklaart ook de tien- en vijfvoudige symmetrieën.
Van zichzelf zijn regelmatige vijfhoeken en tienhoeken juist uiterst ongeschikt om vakken mee te vullen. Regelmatige drie-, vier-, en zeshoeken laten zich wel moeiteloos aaneenleggen tot een vlakvulling. De resulterende repeterende patronen zijn vervolgens drie-, vier- of zesvoudig symmetrisch, wat betekent dat ze er hetzelfde uitzien na een draaiing over een derde, een vierde of een zesde cirkel. Vijfhoeken en hoger-dan-zeshoeken kun je niet op die manier aan elkaar leggen, zo is wiskundig bewezen. Wel kun je, zo werd in de jaren zeventig van de vorige eeuw aangetoond, met andere vormen vijfvoudig symmetrische patronen leggen die oneindig uit te breiden zijn, maar zichzelf nooit herhalen, zogenaamde 'quasikristallijne betegelingen'.
Deze patronen veroorzaakten een rage onder wiskundigen en ook natuurkundigen, die de vijfvoudige symmetrieën terugvonden in echte kristallen van metaallegeringen. Ook de middenstand profiteerde met fraaie quasikristallijne patronen op tafelkleden en behangpapier. Nu blijkt dat deze bijzondere patronen ruim vijf eeuwen ouder zijn, en voor het eerst werden toegepast ter meerdere eer en glorie van Allah. Op de wanden van het Darb-i Imam-heiligdom in Isfahan van 1453 vonden Lu en Steinhardt een bijna perfect quasikristallijn patroon, gemaakt met de sjabloontegels. Alleen op een paar plaatsen zitten er onvolkomenheden in het patroon, maar dat kan ook door een onhandige handwerksman komen, en is altijd plaatselijk te herstellen.
In hoeverre de architecten deze bijzondere patronen wiskundig doorgrondden is niet bekend, maar dat het om een toevalstreffer gaat, lijkt onwaarschijnlijk. De vondst van nog meer, liefst perfect quasikristallijne, girih-versieringen zou daarover uitsluitsel kunnen brengen.
Bruno van Wayenburg
Bron:
Peter J. Lu, Paul J. Steinhardt, 'Decagonal and Quasi-Crystallinge Tilings in Medieval Islamic Architecture', Science, 23 november 2006
terug naar de Gulden Snede
^