Plato's vijf regelmatige veelvlakken

De vijf regelmatige veelvlakken (ook wel 'Platoonse lichamen' genoemd) zijn vijf ruimtelijke vormen uit de stereometrie (ruimtelijke meetkunde) die samen een unieke groep vormen: de tetraëder, hexaëder (kubus), oktaëder, dodekaëder en ikosaëder. Zij zijn de enige ruimtelijke vormen die de volgende eigenschappen bezitten:

1. de vijf regelmatige veelvlakken zijn:
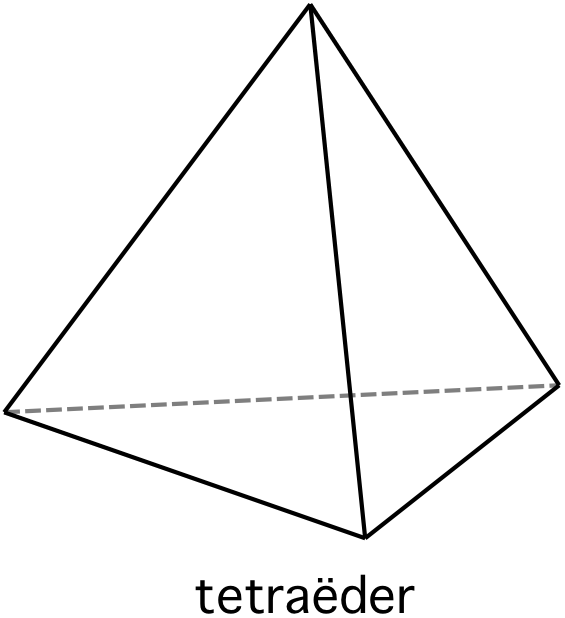
    tetraëder  (4 gelijkzijdige driehoeken)
    hexaëder  (6 vierkanten)
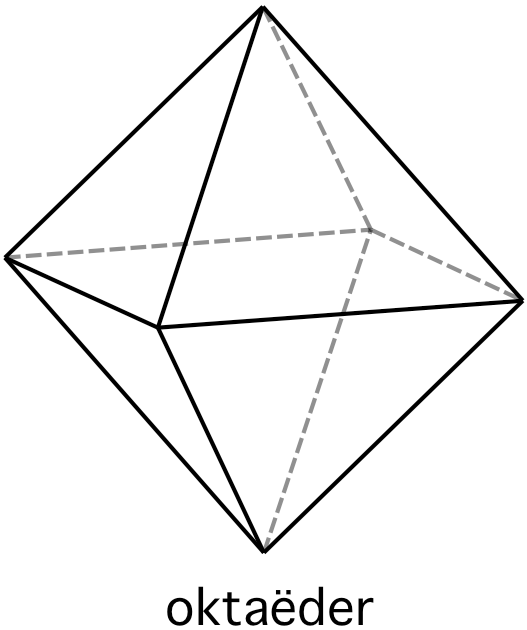
    oktaëder  (8 gelijkzijdige driehoeken)
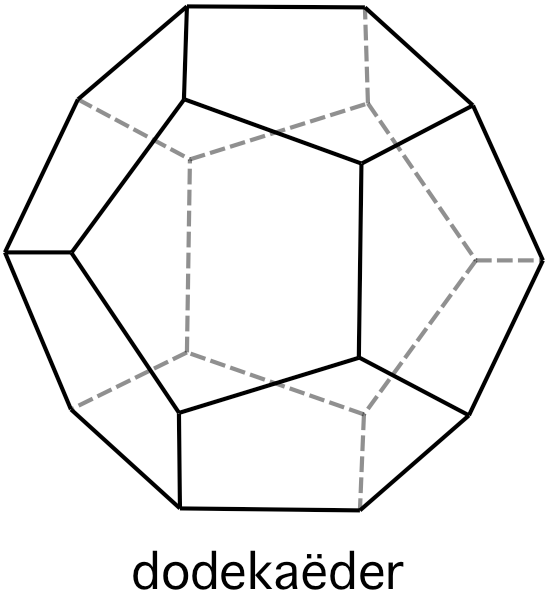
    dodekaëder  (12 vijfhoeken)
    ikosaëder  (20 gelijkzijdige driehoeken)

2. de unieke eigenschappen:
    alle vlakken zijn gelijk
    alle hoeken zijn gelijk
    alle ribben zijn gelijk
ze bezitten alle een
    ingeschreven bol
    omgeschreven bol
    middenbol daartussen

De tetraëder, hexaëder (kubus) en ikosaëder waren al aan Pythagoras bekend, de oktaëder werd later door zijn leerlingen, de pythagoreeërs gevonden, terwijl Aristoteles als laatste de vijfde vond (de kwintessense): de dodekaëder.

Inhoud
1. De vijf regelmatige veelvlakken
2. De veelvlakken en de gulden snede
3. De veelvlakken als verstrengelde eenheid

1. De vijf regelmatige veelvlakken

tetraëder
viervlak

hexaëder (kubus)
zesvlak

oktaëder
achtvlak

dodekaëder
twaalfvlak

ikosaëder
twintigvlak

Naar: H. Lauwerier - Symmetrie, kunst en computers
terug naar de Inhoud

2. De veelvlakken en de gulden snede

Alle regelmatige veelvlakken hangen samen met de gulden snede in de volgende vorm:

Drie gulden rechthoeken (lengte en breedte verhouden zich als de gulden snede) in een driedimensionale samenhang in elkaar geschoven, die binnen vier van de vijf regelmatige veelvlakken past en bij de tetraëder in het midden aan de ribben raakt.

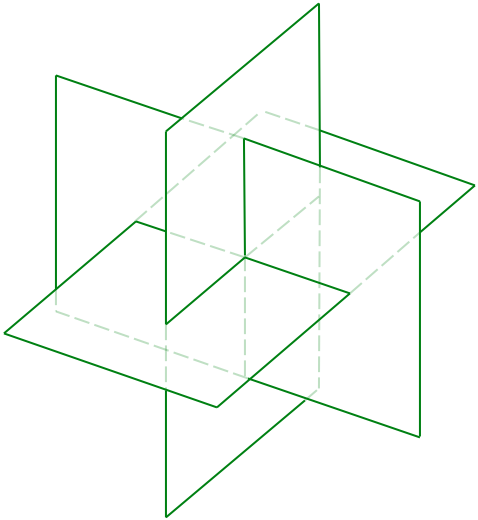
Drie gulden rechthoeken in een driedimensionale samenhang in elkaar geschoven, raken de ribben van de tetraëder in het midden.
De tetraëder en de kubus hangen nauw met elkaar samen: de diagonalen van de kubus vormen de tetraëder.

Drie gulden rechthoeken in een driedimensionale samenhang in elkaar geschoven, raken in het midden aan de vlakken van de kubus.

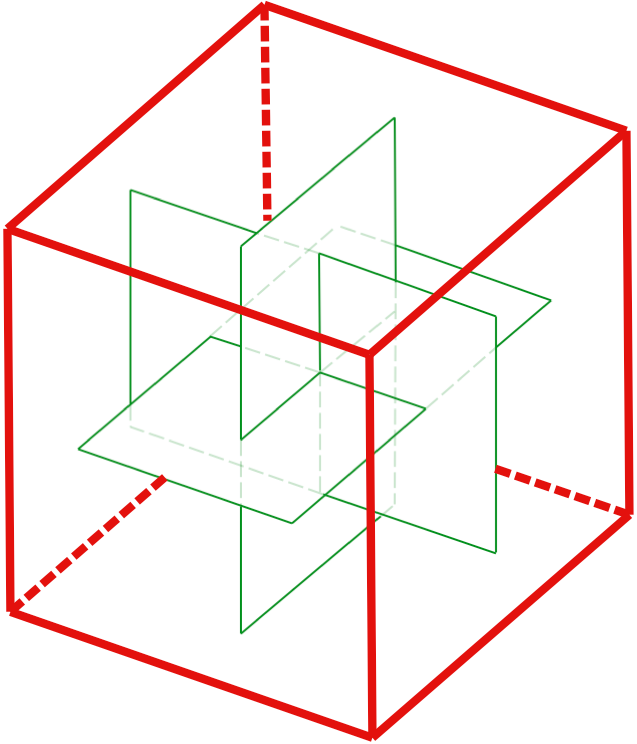
Drie gulden rechthoeken in een driedimensionale samenhang in elkaar geschoven, raken de ribben van de oktaëder op de plaats van de gulden snede.

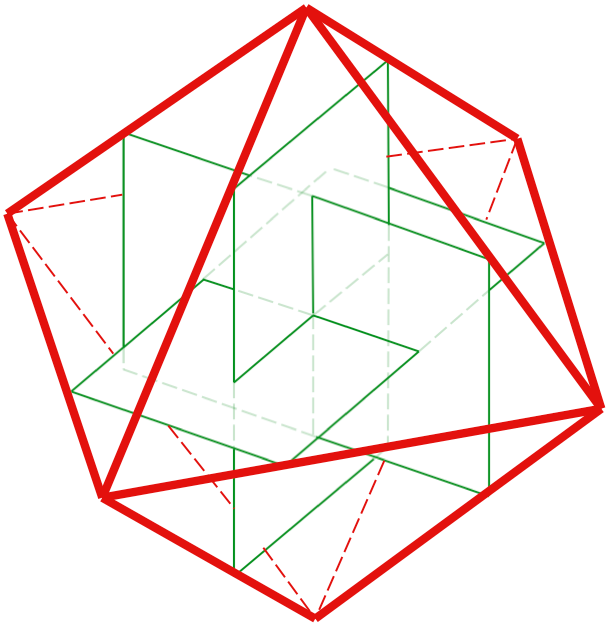
Drie gulden rechthoeken in een driedimensionale samenhang in elkaar geschoven, raken aan de middelpunten van de vlakken van de dodekaëder.

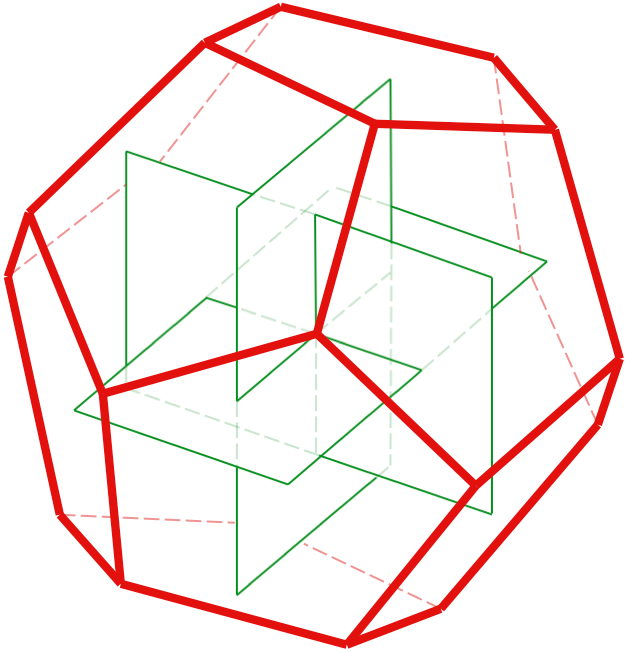
Drie gulden rechthoeken in een driedimensionale samenhang in elkaar geschoven, vallen samen met de ribben van de ikosaëder.

terug naar de Inhoud

3. De veelvlakken als verstrengelde eenheid

De kubus aan de buitenkant
De vijf regelmatige veelvlakken hangen zoals getoond alle samen met de gulden snede én zij passen tenslotte op één manier allemaal in elkaar:

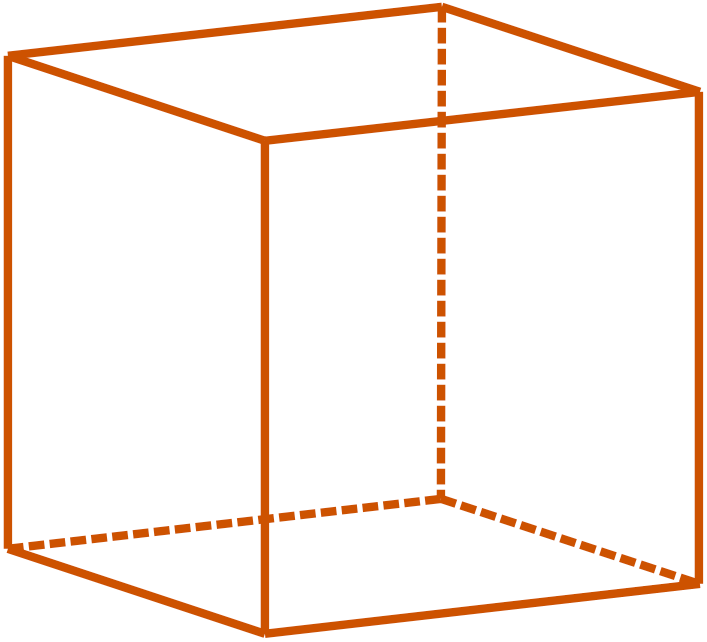
Tetraëder in kubus
Alle ribben van de tetraëder passen op de diagonalen van alle vlakken van de kubus. De tetraëder is een eigenschap van de kubus.

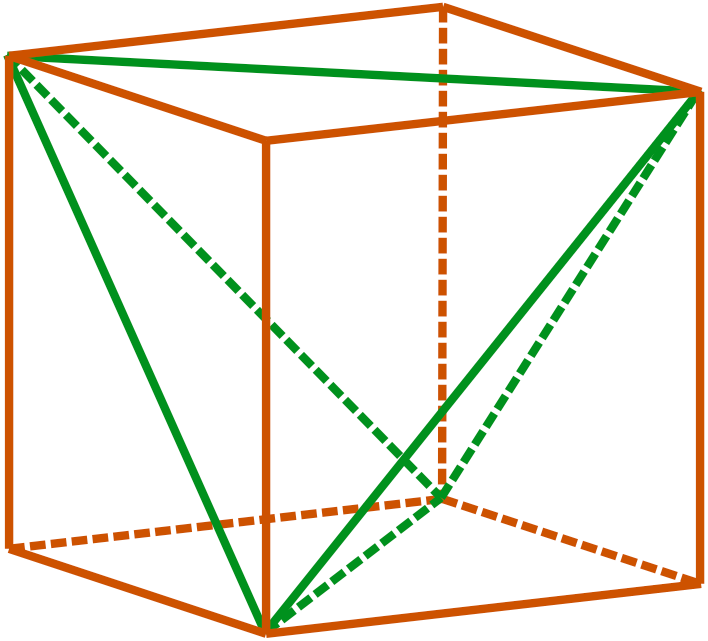
Oktaëder in tetraëder in kubus
Alle hoekpunten van de oktaëder passen op de middens van alle ribben van de tetraëder; én de hoekpunten van de oktaëder raken de middens van de zijvlakken van de kubus.

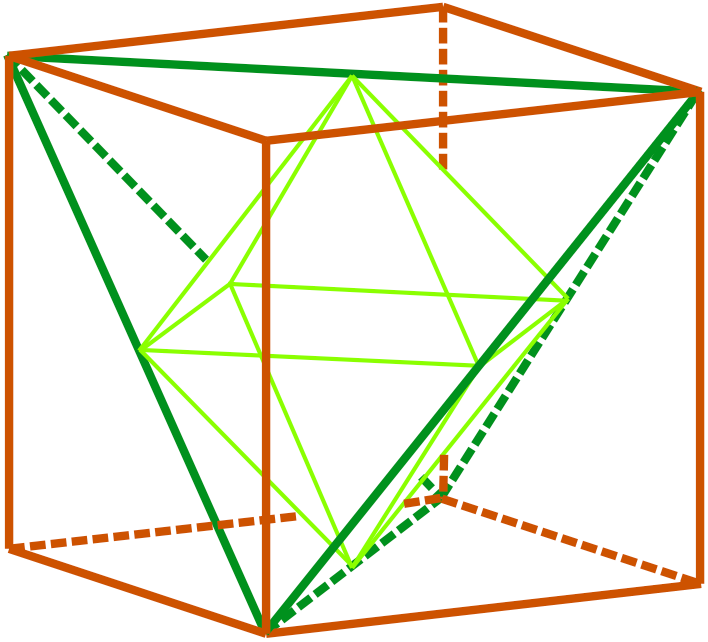
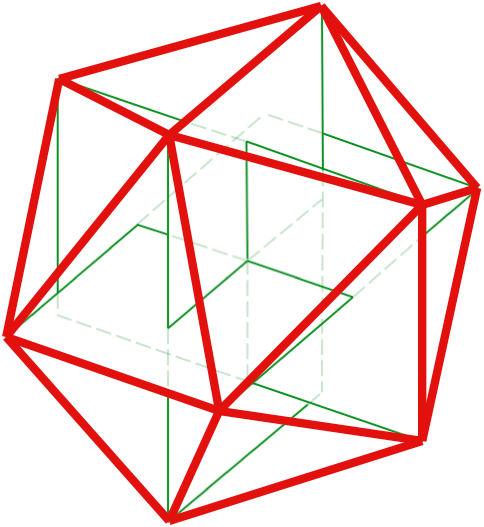
Ikosaëder in oktaëder in tetraëder in kubus
Alle hoekpunten van de ikosaeder passen op de ‘gulden snede plaats’ op alle ribben van de oktaëder.

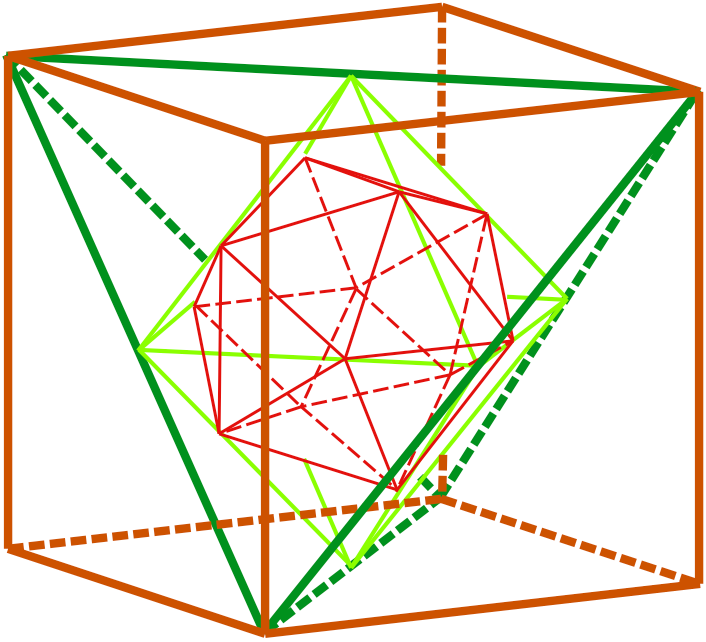
Dodekaëder in ikosaëder in oktaëder in tetraëder in kubus
Alle hoekpunten van de dodekaëder passen op de middens van alle vlakken van de ikosaëder.

De dodekaëder vormt de kern van het vijftal, de kwintessense.

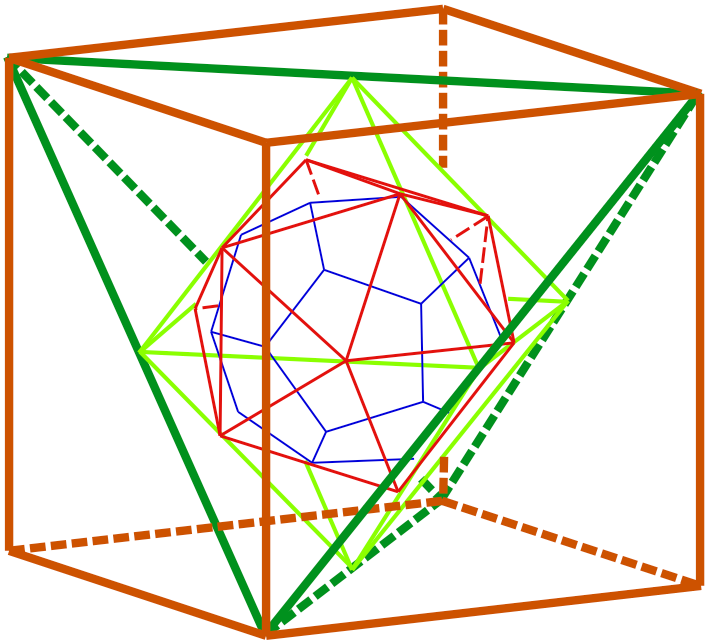
De veelvlakken vormen een eenheid, een innige samenhang doordat zij met elkaar zijn verstrengeld.
kubus - donkerbruin
tetraëder - donkergroen
oktaëder - lichtgroen
ikosaëder - rood
dodekaëder - blauw

terug naar Pythagoras en Plato

terug naar het weblog

^