Bewijs van de Stelling van Pythagoras
De Stelling van Pythagoras: in een rechthoekige driehoek met zijden a, b en c is de som van het kwadraat van de rechthoekszijden a en b gelijk aan het kwadraat van de schuine zijde c.
Meetkundig bewijs:
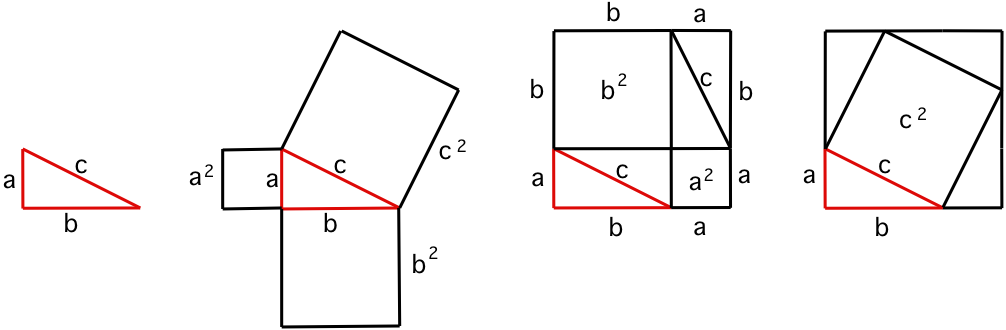
Teken om de driehoek abc de vierkanten die het kwadraat van de zijden weergeven: a², b² en c².
Teken vervolgens een vierkant met zijden a+b en teken daarin de driehoek abc.
Vanuit de hoekpunten van de driehoek kan het vierkant worden verdeeld en twee vierhoeken a² en b²; in het overblijvende oppervlak kunnen 4 driehoeken abc worden getekend.
Teken een tweede vierkant met zijden a+b en daarin vier maal de driehoek abc, maar vanuit de vier hoekpunten. Wat overblijft is het vierkant c².
Van het oppervlak van beide vierkanten met zijden a+b zijn 4 driehoeken abc afgetrokken, waardoor de overblijvende oppervlakten gelijk zijn, m.a.w. a² + b² = c².
Algebraïsch bewijs:
De zijden van het grote vierkant zijn (a+b) en de oppervlakte (a+b) × (a+b) = (a+b)².
De oppervlakte van het grote vierkant is ook gelijk aan de som van de oppervlakken van de vier driehoeken (4 × ½ab) plus de oppervlakte van het binnenste vierkant, c².
Algebraïsch geldt: (a+b)² = (4 × ½ab) + c².
Het kwadraat links geeft uitgewerkt: a2 + 2ab + b2 en (4 × ½ab) + c² = 2ab + c².
Invullen in de vergelijking geeft: a² + 2ab + b² = 2ab + c²,
2ab kan worden afgetrokken, m.a.w. a² + b² = c².
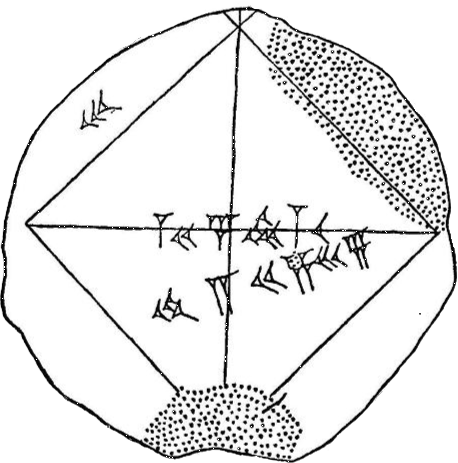
kleitablet met de stelling
Maar Pythagoras zelf of zijn leerlingen leverden wel het bewijs ervoor, waardoor de naamgeving toch steekhoudend is.
Het eerste stel oplossingen is: 3, 4 en 5
want 3² + 4² = 9 + 16 = 25 = 5²
terug naar Pythagoras' getallenleer
^