The golden ratio predicted: vision, cognition and locomotion as a single design in nature, Adrian Bejan
Adrian Bejan, Int. J. of Design & Nature and Ecodynamics. Vol. 4, No. 2 (2009) 97-l04
J. A. Jones Distinguished Professor, Duke University, North Carolina, USA.
© 2009 WIT Press, www.witpress.com
ISSN: 1744-3687 (paper format), ISSN: 1744-3679 (online), https://journals.witpress.com
DOI: 10.2495/D&NE-V4-N2-97-104
ABSTRACT
Shapes with length/height ratios (L/H) close to 3/2 are everywhere and give the impression that they are being 'designed' to match the golden ratio (φ): 1.618. Here I show that these shapes emerge as part of an evolutionary phenomenon that facilitates the flow of information from the plane to the brain, in accordance with the constructal law of generation and evolution of design in nature.
The time required by the eyes to scan a rectangular area L x H is minimal when the shape is L/H = VL/VH, where VL and VH are the horizontal and vertical scanning speeds. This special shape is such that the time for scanning long and fast (L/VL) is the same as the time for short and slow (H/VH). I also show that VL/VH is approximately 3/2 and that consequently L/H ~ 3/2.
This natural evolutionary design is an integral part of the universal constructal design that facilitates the flow of the biosphere, hydrosphere and atmosphere on earth. Vision, cognition and locomotion are features of a single design for movement of animal mass with easier and easier access in time, all over the globe.
Keywords: big history, cognition, constructal law, golden mean, golden number golden ratio, locomotion, vision.
1 IMAGES THAT BREATHE AND FLOW
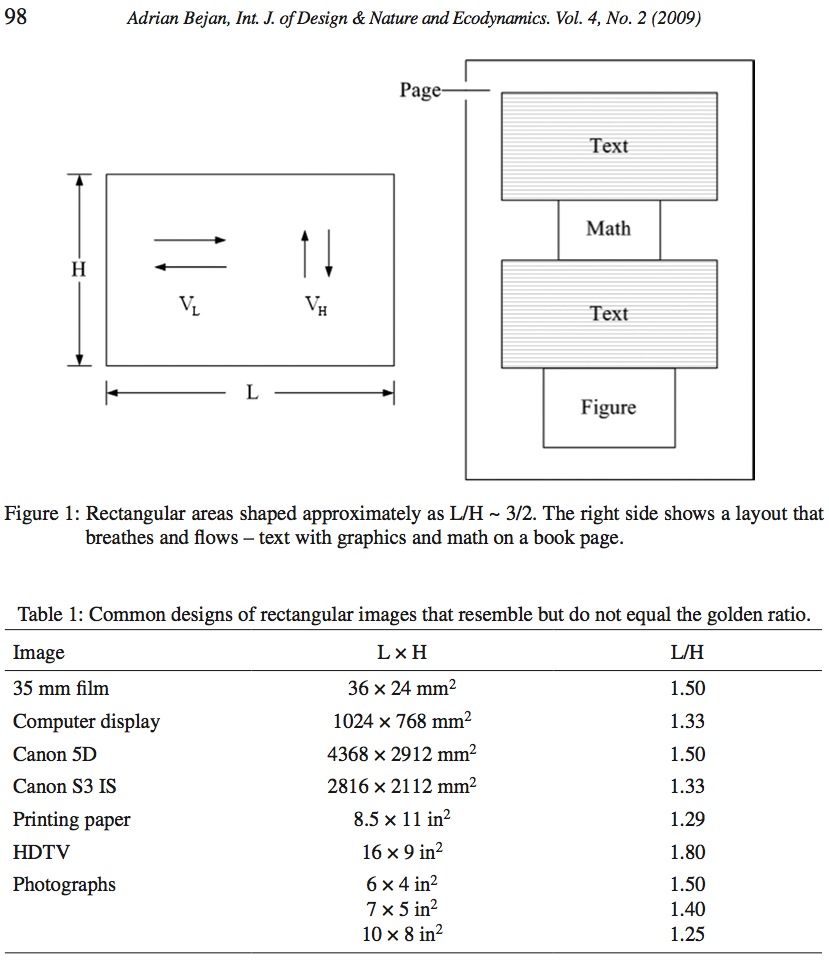
I am used to making my drawings to look almost square, a little wider than tall. The first thought is that this comes naturally because of my training. At age 10, in art school my drawing paper and the canvas were that way, a rectangular surface with the horizontal dimension 'L' larger than the vertical dimension 'H' (Fig. 1, left). Ten years later, in engineering school, the drawing board was oriented the same way.
While writing books, I received the same advice from the artists at John Wiley & Sons. Tall figures clash with the horizontal text, and this clash makes both unattractive. Looking back, I see the L ≥ H everywhere. It is in the shapes of the figures on the page, and in the shapes of the paragraphs - the blocks of text that we tend to read at a glance because we lack time. They all look like the cinema screens (Fig. 1, right). The text 'breathes' when its paragraphs are not too long, i.e. not too tall. A frequent editorial advice to an aspiring author is 'use shorter paragraphs'.
These lessons are not new. It has been known for a very long time that certain shapes 'breathe' and 'flow' better than most other shapes. Shapes mean proportions, such as the ratio L/H ~ 3/2 shown in the rectangles of Fig. 1 and Table 1. When we go to the stadium we prefer to sit on the side, not on the end. This 'flow quality' of the drawing is undeniably linked to the beauty and usefulness that we detect in the image.
2 THE GOLDEN RATIO PHENOMENON
The connection between proportions and good looks has generated a lot of discussion in science because of an accidental occurrence: the shapes that we see in the design of books, paintings and edifices are approximated by a rectangle shaped such that its L/H is equal to the 'golden ratio' φ = (1 + 51/2)/2 = 1.618. The φ number is the result of dividing a segment into two segments (L + H) such that (L + H)/L = L/H. The fact that generation after generation our own drawings appear to favor proportions that resemble the golden ratio has fueled an entire literature and mysticism [1]. This activity is further energized by the fact that the golden ratio φ has not been deduced from a physics principle.
The race to discover φ is misdirected because the physics phenomenon is not φ itself. No one has found and measured φ on an object in nature (φ is not like π, which is measurable by dividing the measured circumference by the measured diameter). The physics phenomenon is the emergence of shapes that resemble φ.
3 CONSTRUCTAL FLOW CONFIGURATIONS: VISION AND COGNITION
Here is how to predict the physics phenomenon. The physics principle is the constructal law of generation of flow configuration in nature [2, 3]. The key question is: Why do the shapes with L/H ~ 3/2 appear to 'breathe' and 'flow'? What flows when we look at a page with text, math and art? Information flows, as images, from the page to the brain.
According to the constructal law, 'for a finite-size flow system to persist in time (to live) it must evolve in time such that it provides easier access to the currents that flow through it' [2-4]. The system that flows from the plane (the page) to the brain during reading (and from the brain to the page during writing and painting) has been morphing in the constructal-law direction naturally.
The evidence in support of this principle is massive. The architecture of the brain consists of bundles and bundles of constantly forming and adjusting tree-shaped flows. The reason is that tree-shaped architectures provide easier and easier point-volume and point-area access [4-8]. This also holds for the connection between each elemental volume of the brain and the rest of the brain volume, and vice versa [9]. The visual sensors and nerves in the retina are configured in the same way, as dendrites, in order to provide greater access between one surface (the retina) and one point (the optic nerve).
The external architecture of this flow system has also been morphing in the constructal-law direction of flow configuration generation in time, toward easier flowing. Here again the evidence is massive. The evolution of writing, toward simplicity and universality (one alphabet), is one phenomenon of design generation [10]. The evolution of languages, and the emergence of English as a global language, is another example. The evolution of book design, library design, currency design, photography, eyeglasses, dashboard and computer screen design (Table l) is the same phenomenon of facilitating the flow of information between the page and the brain.
4 THE CONSTRUCTAL SHAPE OF THE SCANNED IMAGE
Consider now the area H x L shown in Fig. 1 (left). The shape of the image is part of the architecture of the information flow system, and it is free to change. The eye must scan the rectangular area H x L, and it must do it with the greatest ease, i.e. in the shortest time.
In the simplest description, to scan is to sweep the image completely, horizontally and vertically.
The horizontal sweep covers the length L with the average speed VL (averaged over several saccades).
The horizontal sweep time is tL = L/VL. The vertical sweep covers the distance H with the averaged speed VH and time tH = H/VH.
The total time required to scan the image is of order t = L/VL + H/VH. The area of the image is fixed (A = HL), but the shape of the image (L/H) is arbitrary. The total time is t = L/VL + A/(LVH), and it is minimal when L = (AVL/VH)1/2, which represents this rectangular shape:
L/H = VL/VH (1)
The first implication of this result is that the shape of the image matters to how the image is perceived, understood and recorded. The second implication is that when the image is shaped according to eqn (1), the horizontal sweep takes just as long as the vertical sweep,
tL = tH (2)
The partitioning of the scanning time equally into tL and tH is a common design feature for flow access (e. g. it is found in the design of city traffic, river basins and lungs [11]). In the present case, if L ≥ H then VL ≥ VH, such that tL = tH means that the time to scan long and fast must be the same as the time to scan short and slow.
The third implication is that L/H must indeed be a number greater than 1 because the ratio VL/VH is expectedly greater than 1, as we will see below. We scan things easier on the horizontal than on the vertical. The reader can verify this by performing the following test: to scan horizontally is easy, while to scan vertically triggers the urge to tip the head.
The eye mechanics literature [12-23] contains information on horizontal eye movement (VL), but not on vertical movement (VH). This record too is a consequence of the fact that our perceived world is roughly a horizontal tableau. Our supply of images reflects the orientation of the landscape. Danger comes to the animal from the sides and from behind, not from above, and not from below.
With organs for vision, the animal minimizes danger from ahead and from the sides. This is the link between vision and locomotion, and the fulcrum of the single design of animal movement on earth. We return to this observation in section 5.
Like the L/H ratio of eqn (1), the positioning of our two eyes on a horizontal axis is a constructal-law design feature. The horizontal orientation of the eye-eye axis (not the vertical, not the inclined)
is the most facile for the flow of visual information from our horizontal environment to the brain.
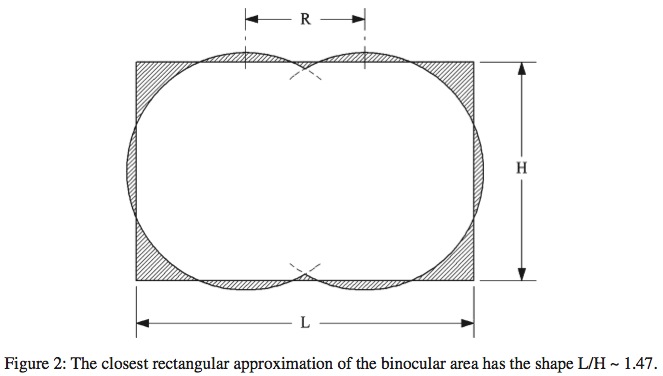
The horizontal shape of our field of vision is approximated by the construction shown in Fig. 2.
The length scale of the disc (R) is due to the distance between the eyes. The superposition of the two discs is the binocular area. If one eye sweeps one disc horizontally (length 2R, time tL) and vertically (length 2R, time tH = tL), then, because of the superposition of the two discs, the horizontal length scanned by the two eyes is 3R. The horizontal and vertical speeds are VL = 3R/tL and VH = 2R/tH, and because tL = tH, the ratio of speeds is VL/VH = 3/2.
The binocular area can be approximated by superimposing on it a rectangle with the right shape and size. Two approximations are closely represented by the same rectangle in Fig. 2. The first is the rectangle that mimics the closest curvilinear contour of the binocular area: the sum of the areas formed between the rectangular and the curvilinear contours is minimal. The dimensions of this rectangle are L = 2.768 R and H = 1.876 R, and its shape is L/H = 1.475. lf in addition to minimizing the total area of mismatch between the two shapes the rectangular area must be equal to the binocular area, the best rectangular shape is L = 2.724 R, H = 1.856 R and L/H = 1.468. This second shape is practically the same as the first.
5 VISION, COGNITION AND LOCOMOTION AS A SINGLE DESIGN
In conclusion, humans scan the world on a two-dimensional screen approximated by a rectangle with the shape L/H ~ 3/2. We scan the long dimension faster than the vertical dimension, in such a way that to scan long and fast (L, VL) takes the same time as to scan short and slow (H, VH). This is the best flowing configuration for images from plane to brain, and it manifests itself frequently in human-made shapes that give the impression that they were 'designed' according to the golden ratio (Table l).
The many occurrences of such shapes support the principle-based explanation advanced in this paper. Even more, the technological evolution process that governs the occurrence of these shapes on paper and on screens is driven by the same constructal law that generates the biological L/H ratio of the scanned image. For example, old computer and TV screens had aspect ratios close to l.33 (as in Table 1), this as a first-cut design. However, as new technologies loosen the design restrictions, the screens morph toward wider shapes, with L/H values closer to 3/2. This is one example of technology evolution, and it is in line with the other examples of technology evolution detailed in Ref. [8]: the cooling of high-density electronics and the emergence of distributed energy systems on earth.
The golden-ratio phenomenon and its constructal-law prediction illuminate the oneness of the integrative design of the movement of biological mass on earth. Shapes that resemble the golden ratio facilitate the scanning of images and their transmission through vision organs to the brain. The speeding up of this flow goes hand-in-hand with the dendritic architectures of the nervous system in the eye and the brain. Dendrites maximize the rate of point-volume flow of information inside finite volumes, and the rate at which new point-volume connections can occur naturally in the brain. The name of this constructal evolution of brain architecture, every minute and every moment, is cognition - the phenomenon of thinking, knowing and thinking again, better. 'Getting smarter' is the constructal law in action.
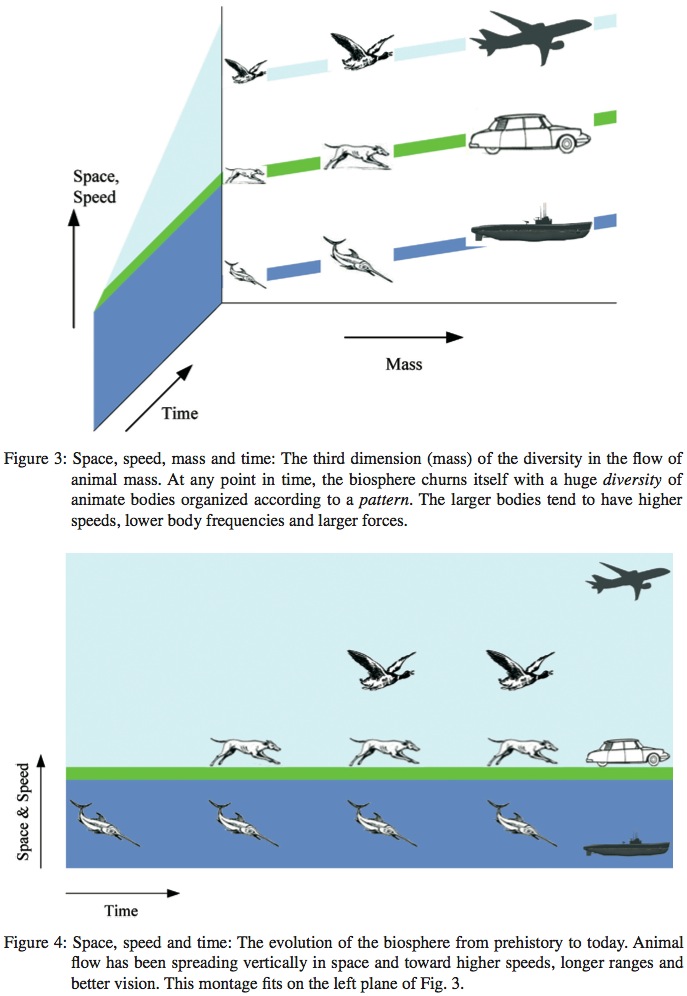
Vision and cognition are one, and they are demanded by the constructal law applied at the scale of the earth. Animal mass and water mass (in river basins) are flow systems with configurations and rhythms that facilitate the flow of mass on earth. From this physics application of the constructal law, we predicted all the scaling rules of animal locomotion [24, 25], and the evolution of speed limits in athletics [26]. For example, larger animals must have higher speeds calculated with formulas in which speeds are proportional to their body masses raised to the power l/6, and body movement frequencies (stride, flapping, fishtailing) are in proportion to body masses raised to - l/6. These predictions agree with all the known speed-mass data for ilyers, land animals and swimmers. This is summarized qualitatively in the back plane of Fig. 3. The actual clouds of speed-mass data are available in Figure 7 of Ref. [24].
Locomotion design is a manifestation of the constructal law, and it has been perfecting itself throughout the history of biological forms and flows systems on earth (i.e. throughout 'big history').
This is why animal locomotion first emerged in the oceans, spread on land and later rose in the air, not the other way around.
The time direction of this evolution has been toward higher speeds, and it is shown qualitatively in Fig. 4, which is a detail of the side plane of Fig. 3. More movement and more mixing of the earth (upward in space) has always been aligned with time, more speed, and more space traveled per unit of animal mass and useful energy consumed.
The big jump in the perfecting of the animal locomotion design was the emergence of the organ for vision (the eye). This has made the flow of animal mass much more efiicient, faster and enduring, because with vision and cognition the flow of animal mass designs for itself ceaselessly better channels to flow: straighter, safer, with fewer obstacles and predators. This step change in the animal locomotion design is known as the Cambrian explosion (ca. 530 million years ago), and its time arrow is in complete accord with the constructal law, toward more space, speed and mixing of the earth's crust. The Cambrian 'explosion' means all these things. The animal design with vision and cognition came after the animals without vision and cognition, not the other way around.
ACKNOWLEDGEMENTS
This work was supported by a grant from the National Science Foundation. I thank my colleagues for their help on this article: Prof. John Petrowski (Duke Medical School, Eye Center), Prof. Sylvie Lorente (University of Toulouse, INSA), Dr. Atit Koonrisuk (Suranaree University of Technology, Thailand) and Prof. Kuan-Min Wang (Tatung Institute of Technology, Taipei, Taiwan).
REFERENCES
[1] Livio, M., The Galden Ratio, Broadway Books: New York, 2002.
[2] Bejan, A., Advanced Engineering Thermodynamics, 2nd edn, Wiley: New York, 1997.
[3] Bejan, A., Shape and Structure, from Engineering to Nature, Cambridge University Press: Cambridge, UK, 2000.
[4] Bejan, A. & Lorente, S., Constructal theory of configuration generation in nature and engineering. J. Appl. Phys., 100, 2006, 041301.
[5] Reis, A.H., Constructal theory: from engineering to physics, and how flow systems develop shape and structure. Appl. Mech. Rev., 59, pp. 269-282, 2006.
[6] Miguel, A.F., Constructal pattern formation in stony corals, bacterial colonies and plant roots under different hydrodynamics conditions. J. Theor. Biol., 242, pp. 954-961, 2006.
[7] Reis, A.H., Constructal view of scaling laws of river basins. Geomorphology, 78, pp. 201-206, 2006.
[8] Bejan, A. & Lorente, S., Design with Constructal Theory, Wiley: Hoboken, NJ, 2008.
[9] McIntosh, A.R., Towards a network theory of cognition. Neural Networks, 13, pp. 861-870, 2000.
[10] Amoozegar, C., Constructal theory of written language. Constructal Theory of Social Dynamics, eds A. Bejan & G.W. Merkx, Springer: New York, 2007.
[11] Lewins, I., Bejan's constructal theory of equal potential distribution. Int. J. Heat Mass Transf., 46, pp. 1541-1543, 2003.
[12] Ferman, L., Collewijn, H., Jansen, T.C. & Van den Berg, A.V., Human gaze stability in the horizontal and torsional direction during voluntary head movements, evaluated with a three-dimensional scleral induction coil technique. Vision Res., 27, pp. 811-828, 1987.
[13] Collewijn, H., Erkelens, C.J. & Steinman, R.M., Binocular co-ordination of human horizontal saccadic eye movements. J. Physiol., 404, pp. 157-182, 1988.
[14] Thorpe, S., Fize, D. & Marlot, C., Speed of processing in the human visual system. Nature, 381, pp. 520-522, 1996.
[15] Schiller, P.H. & Chou, I.-h., The effects of frontal eye field and dorsomedial frontal cortex lesions on visually guided eye movements. Nature Neuroscience, 1(3), pp. 248-253, 1998.
[16] Pirolli, R & Card, S., Information foraging. Phychological Review, 106(4), pp. 643-675, 1999.
[17] Moore, S.T., Hirasaki, E., Cohen, B. & Raphan, T., Effect of viewing distance on the generation of vertical eye movements during locomotion. Exp. Brain Res., 129, pp. 347-361, 1999.
[18] Castet, E. & Masson, G.S., Motion perception during saccadic eye movements. Nature Neuroscience, 3(2), pp. 177-183, 2000.
[19] Land, M.E. & McLeod, R, From eye movements to actions: how batsmen hit the ball. Nature Neuroscience, 3(12), pp. 1340-1345, 2000.
[20] Turano, K.A. & Heidenreich, S.M., Eye movements affect the perceived speed of visual motion.Vision Res., 39, pp. 1177-1187, 1999.
[21] Martinez-Conde, S., Macknik, SL. & Hubel, D.H., The role of fixational eye movements in visual perception. Nature Reviews, Neuroscience, 5, pp. 229-240, 2004.
[22] Kirchner, H. & Thorpe, S.J., Ultra-rapid object detection with saccadic eye movements: visual processing speed revisited. Vision Res., 46, pp. 1762-1776, 2006.
[23] Bauerlein, M., Online literacy is a lesser kind. The Chronicle Review, 54(31), p. B7, 2008.
[24] Bejan, A. & Marden, J.H., Constructing animal locomotion from new thermodynamics theory.
American Scientist, 94, pp. 342-349, 2006.
[25] Bejan, A. & Marden, J.H., Unifying constructal theory for scale effects in running, swimming and flying. Journal of Experimental Biology, 209, pp. 238-248, 2006.
[26] Charles, J.D. & Bejan, A., The evolution of speed, size and shape in modern athletics. Journal of Experimental Biology, 212, pp. 2419-2425, 2009.
[27] Bejan, A., Lorente, S. & Lee, J., Unifying constructal theory of tree roots, canopies and forests.
Journal of Experimental Biology, 254, pp. 529-540, 2008.
[28] Bejan, A., Advanced Engineering Thermadynamics, 3rd edn, Wiley: Hoboken, pp. 774-779, 2006.
terug naar het literatuuroverzicht
^