Jan Poortenaar - De gulden snede en goddelijke verhouding

Vierde druk, 1947
Uitgeverij In Den Toren, Naarden
Toren Reeks 8-9

"Componisten projecteren het oneindige in het eindige."
Edvard Grieg (1843-1907), Noors componist

Inhoud


Jan Poortenaar (1886-1958)
graficus, kunstschilder, aquarellist,
tekenaar, etser, illustrator,
auteur en uitgever
Inleiding, een algemene schoonheidsnorm
Griekenland
Vitruvius: overeenstemming tussen de delen en het geheel - de gulden snede
Constructie van de gulden snede
Regelmatige veelhoeken
De menselijke maat
Luca Pacioli - De Divina Proportione
Bewuste of onbewuste toepassing
Vioolbouw
Papiermaten
De traditie
De geest schept de maat, niet de maat den geest
Over de schrijver
Literatuur

Inleiding, een algemene schoonheidsnorm

Te allen tijde heeft de mensch, die een diepe emotie van schoonheid ervoer, de verrijking beseft welke deze zijn innigste wezen schonk. Daarom is gepoogd, wat de kern dier schoonheid uitmaakte, vast te houden of althans iets ervan op de een of andere wijze zoo te kristalliseeren, dat de eens ondervonden ontroering daaruit een ander maal opnieuw tot leven te brengen zou zijn. Van de oudste beschaving af is dan ook een streven merkbaar, schoonheidsnormen op te zoeken en vast te leggen, de fundamenten waarop een kunstbouwsel rust als het ware in teekening te brengen.
Het schoone, het welstandige zocht men te fixeeren in bepaalde verhoudingen en zulk een maat, welke achter de uiterlijke, voor iedereen waarneembare vormen leeft en slechts voor ingewijden, kunstenaars-vaklieden daar uit te lichten valt, zulk een regel noemde men sedert de Grieken, met hun benaming, een 'canon'. Zulk een grondregel van ideale verhoudingen zou dan een voedingsbodem voor latere kunstuitingen kunnen zijn. De Grieksche beeldhouwer Polykleitos reeds stelde er een op voor de ideale menschengestalte. (5)

Ongetwijfeld zijn er bepaalde grondslagen, al zijn het geen nauwkeurige maten die de hoofdverhoudingen van Europa's Gothische kathedralen bepalen; zoo zijn er ook in Arabië's moskeeën, Java's Boeddha-beelden en Egypte's pyramiden gewis vaste grondstelsels belichaamd. Reeds vóór de Grieksche kunst - waaraan wij zooveel te danken hebben - en de Grieksche wiskunde Grieksche normen bepaalden, zocht men in Egypte bases, schoonheidsbronnen met mystieke waarde, waaruit ook de nog komende geslachten zouden kunnen putten. Babyloniërs en andere oude volken deden insgelijks.
Men zocht in die formules steeds waarden te vangen die verder reikten dan het individu - dat immers in onzen huidigen zin nog niet bestond - verder reikte dan persoonlijke vinding, persoonlijke emotie. Men zocht het algemeen schone dat in harmonie met de gansche schepping zou zijn.
Iedere kunstgevoelige Westerling die het Oosten bezocht, weet dat ook thans nog de Oosterling in harmonie met de natuur vermag te bouwen op een wijze, die wij zoo zelfs niet benaderen kunnen; hem zal het hier bedoelde gemakkelijker duidelijk zijn dan den Europeaan, die zijn werelddeel nooit ontsnapt is.

Kunst is steeds uit godsdienst voortgekomen en een getuigenis van het goddelijke, dat in en achter de stoffelijkheid op aarde leeft. Vele godsdiensten nu hebben (6) gemeen, dat zij als goddelijk ervaren wat met de orde der schepping overeenstemt en alles wat tegen de natuurlijke orde der dingen indruischt, als het verkeerde, booze wordt gezien; en bij onze behoefte ons denken concreet en tastbaar voor te stellen, wordt dat booze vaak tot 'de Booze' gematerialiseerd, die dan als demonstratie van zijn onnatuurlijkheid een menschengestalte met afwijkingen: horens, bokspooten, krijgt. Oudtijds zonden de Israëlieten den zondebok de woestijn in, die met de zonden van het volk was beladen.
terug naar de Inhoud

Griekenland

afb. 1 De triomfboog van Septimius
Severus te Rome. De opbouw uit
het kwadraat en den cirkel.
Zochten de priesters-sterrewichelaars der Oudheid de verborgen harmonie van het heelal na te speuren, ook de kunstenaars trachtten die te vinden. Zij waren te zeer daadwerkelijk met verhoudingen bezig om zich niet af te vragen, wat de ideale waren.
Wie aan onze fabrieksschoorsteenen denkt, die buiten alle verhouding uit een landschap oprijzen en het meestal allesbehalve verfraaien, zal toegeven dat in zulk een zoeken naar harmonie iets steekt dat zin heeft. Niet alleen ontbreekt hier harmonie met de natuur, maar zelfs de harmonie der natuur wordt door gemis aan evenredigheid verbroken, waar een of meer van die schoorsteengevaarten hun inderdaad hemel-tergende wanstaltigheid ten toon spreiden.


afb. 2 De middelste boog verdeelt
de hoogte volgens de gulden snede,
de kleine bogen doen het den afstand
van den grond tot de onderste sierlijst.
Niet willekeurige, toevallige, of ook maar uit overweging van nut en doeltreffendheid gekozen verhoudingen dus (7) leiden tot de bedoelde diepe schoonheid, maar alleen zulke proporties, die tot de natuur in een zeker verband staan en ook onderling dezelfde evenredigheid bezitten.
Het werkelijk schone ontstaat dus pas uit evenredigheid: de Grieken, door de eeuwen heen als meesters in edele verhoudingen geprezen en daarin het voorbeeld van alle Europeesche volkeren, stelden dan ook dat het maat-looze, ongebreidelde, de roes, verpersoonlijkt in Dionysos, beteugeling en ordening behoeft om, bij Apollo, tot kunst te worden. Zij duidden dit begrip van evenredigheid met het woord 'ana logia' aan en belichaamden het in een 'canon'.


afb. 3 Bladzijde uit Vitruvius'
'De Architectura' van 1511,
de eerste geïllustreerde uitgave.
Men moet in het gebruik van een canon geen slaafsch navolgen van een dood voorschrift zien. Dat is de Grieksche godengestalte op de academies van het Westen geworden, omdat de Grieksche geest er niet meer bezielend achter stond. De Grieksche kunst zelf was geen onnoozel toepassen van regels, die men uit het hoofd leerde; zij kende de persoonlijke vrijheid, maar om een gemeenschappelijken kern geordend.
In een tijd als de onze, waarin de individueele karaktertrekken van een kunstwerk het hoogst worden aangeslagen - wij vragen het eerst om persoonlijkheid van uiting, wat er geuit wordt komt meestal in de tweede plaats - valt het menigeen moeilijk zich algemeene voor een ieder even klemmende schoonheidsnormen ten denken. (8)

Herinneren wij ons echter Gothische kathedralen, Gregoriaanschen kerkzang, de glasramen, mozaieken en miniaturen der middeleeuwen, dan treedt hier op het eerste plan, wat die uitingen verbindt, niet wat ze onderscheidt. Er mogen nationale trekken zijn aan te wijzen in de Engelsche, Duitsche, Fransche Gothiek, het algemeene stijlkarakter overweegt.

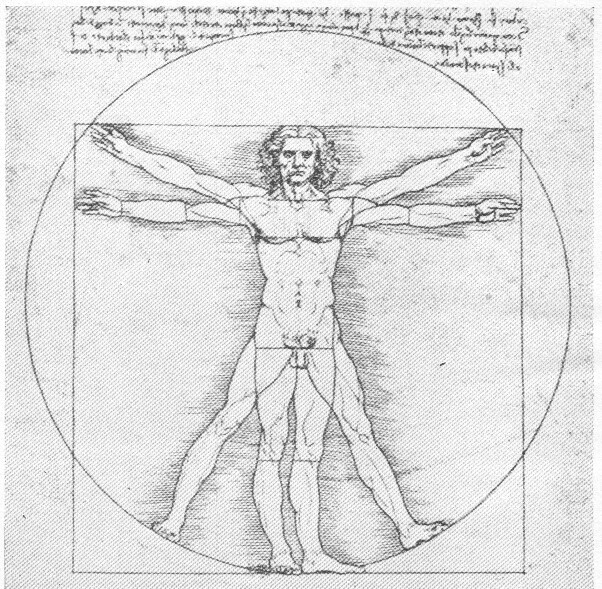
afb. 4 Teekening van Leonardo da
Vinci (Academie, Venetië).
De menselijke figuur past met
uitgestrekte armen in het kwadraat
en den circel van Vitruvius.
Het overweegt zelfs zoozeer, dat het Gothische schrift algemeen als 'Duitsch' bekend staat, terwijl het van Fransche vinding is; doordat het in Duitschland langer in gebruik bleef, heeft men er ten onrechte een specialen naam aan gegeven: het was internationaal en pas later, toen de naties zich deden gelden, heeft men er ten onrechte een nationaal karakter in meenen te zien.

Geestelijke goederen werden in de Middeleeuwen als een gemeenschappelijken schat beschouwd en nog Rembrandt en Dürer putten uit het werk van andere kunstenaars op een wijze, die ons thans ontoelaatbaar voorkomt. Men leefde, en dat was het sterkst in de Middeleeuwen, meer dan wij doen in het besef dat een groot kunstwerk iets zoo machtigs is, dat een enkel menschenleven niet volstaat om het tot vollen rijpdom te brengen, zoodat het den steun eener levende traditie niet kon ontberen.


afb. 5 Dürer's alfabet,
geconstrueerd uit het kwadraat
en den cirkel der Romeinen.
Sterft die traditie af, dan wordt zij conventie, sleur; hoe moeilijk is het, tusschen deze beide de grens te trekken. (9) Wij meenen vaak dat het gemakkelijk is en stellen de persoonlijke inventie boven alles, vergetende, dat daarbij het nietswaardige, gezochte, ons dag in dag uit de oogen verblindt.

Ieder, die muzikaal is, kent het toepassen van een zekere maat, het verschil tusschen haar als zij leeft of dood is: de doode maat is vervelend, de levende maat wekt het rhythme op, dan gebeurt een wonder en stroomen de diepste ontroeringen door de ziel. Zulk een ware maat meende men reeds in oude tijden onder meer in de gulden snede gevonden te hebben. Zij is - het wordt vaak vergeten - wegwijzer, maar geen reisdoel, beginpunt maar geen eindpunt, zij is geen recept om iets moois te maken, maar een kompas, dat een bepaalde richting aanwijst.


afb. 6 Boeddhabeeld (Museum te Sarnath). De vingertoppen van de
hand deelen de hoogte volgens
de gulden snede.
De Babyloniërs verhieven een andere verhouding tot uitgangspunt van hun tempelbouw: den gelijkzijdigen driehoek, de Egyptenaren kenden den z.g. Egyptischen driehoek. En nu meene men niet, hier voor doode antiquiteiten te staan: Berlage schrijft bijvoorbeeld in zijn (in het Duitsch gestelde) 'Grundlagen und Entwickelung der Architektur' dat hij dien 'Egyptischen driehoek' onder meer toepaste bij den bouw van de Beurs te Amsterdam en daarbij zeer bewust die oude verhouding volgde.
Gelijkzijdige driehoeken komen als hexagram met symbolisch-religieuze beteekenis voor op het schild van David. Zoo werden mathematische verhoudingen met geheiligde ideologieën geladen; ook het teeken des kruises was het eeuwen achtereen. (10)

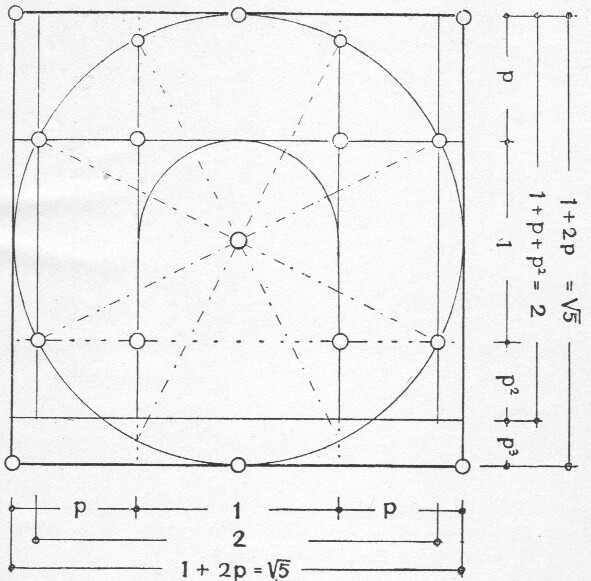
Den Romeinen diende het kwadraat van den ingeschreven cirkel tot uitgangspunt, zooals men bijvoorbeeld bij den Triomfboog van Septimius Severus kan nameten (afb. 1, 2); blijkens gevonden passers (afb. 12) pasten (12) zij eveneens de proporties van de gulden snede toe.
terug naar de Inhoud

Vitruvius: overeenstemming tussen de delen en het geheel - de gulden snede

afb. 7 Boeddhabeeld (Museum te
Sarnath). Opbouw uit kwadraat en
cirkel. Schema: Ernst Möckel.
De Romeinse bouwkundige en theoreticus Vitruvius, die in de eerste eeuw vóór Christus leefde, de auteur van het werk 'De Architectura' (afb. 3), (14) definieert het begrip 'proportie' als: overeenstemming tusschen de samenstellende deelen onderling en overeenstemming ervan met het geheel. (15)

De gulden snede nu geeft zoodanige verhoudingen in de meetkunde en toen de Renaissance herleving der Oudheid bracht, herleefde ook Vitruvius: in 1311 werd zijn werk voor het eerst gedrukt en vond algemeen ingang, zooals vele antieke geschriften en opvattingen. Mannen als Da Vinci (afb. 4) en Albrecht Dürer bestudeerden zijn werk met groote intensiteit.

De Romeinen bouwden onder meer ook het letterschrift waarvan wij ons nog bedienen, de 'capitalis quadrata', hun officieele schriftvorm (afb. 5), uit het kwadraat en den cirkel op; wat de leek heden ten dage een 'drukletter' noemt, heet op de drukkerijen nog altijd een 'romein'.


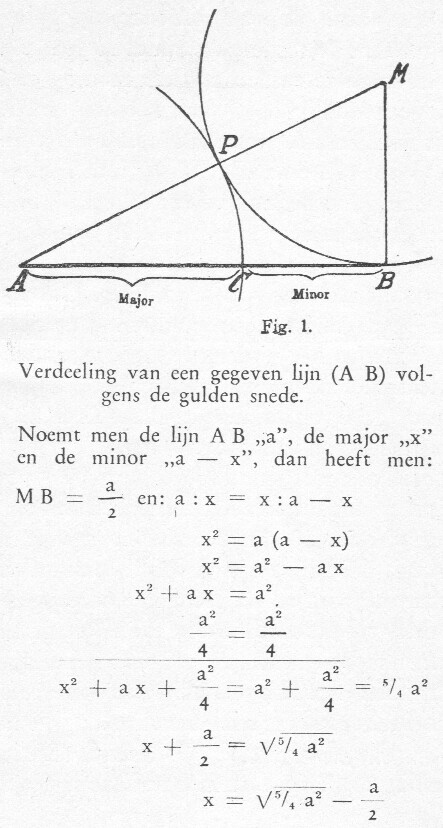
afb. 8 Verdeling van een lijn (AB)
volgens de gulden snede. Noemt
men de lijn AB 'a', de major 'x' en
de minor 'a-x', dan heeft men
MB = a/2 en a:x = x:(a-x)
Toen Dürer in zijn 'Underweysung der Messung mit Zirckel (passer) und Richtscheydt' (lineaal) schreef (1525) construeerde hij het alfabet naar het Romeinsche voorbeeld uit cirkel en kwadraat, in Italië deden Da Vinci en Pacioli, in Frankrijk deed Geofrey Tory hetzelfde, de laatste paste er reeds het tiendeelig stelsel bij toe, dat hij van Apollo en de negen Muzen afleidde ('Champfleury', Parijs, 1536).

Den opbouw uit kwadraat en cirkel treft men trouwens ook in het Oosten aan, meten wij bijvoorbeeld een Boeddha-beeld, dan bevinden wij dat die als grondslag dienden, terwijl de hoogte van het grondvlak tot de vingertoppen en vandaar tot boven aan den aureool de verhoudingen der gulden snede aangeeft (afb. 6, 7). (18)
terug naar de Inhoud

Constructie van de gulden snede
Men vindt deze proporties in onze, d.w.z. de Grieksche meetkunde van Euclides: om een lijn AB volgens de gulden snede te verdeelen (afb. 8), richt men op een harer uiteinden een loodlijn op die half zoo lang is: BM. Men verbindt nu A met M, waarna men met M als middelpunt M op AM omcirkelt.
Zoo vindt men het punt P.


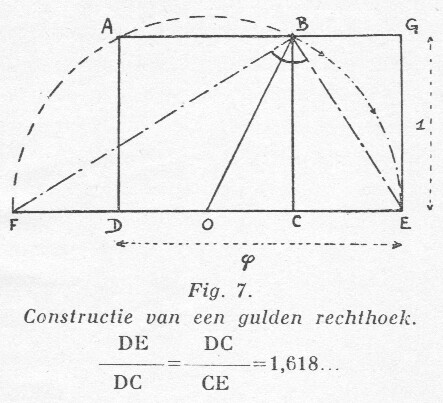
afb. 9 Constructie van
een gulden rechthoek.
DE/DC= DC/CE = 1,618...
Cirkelt men nu het andere deel van A de schuine zijde, om op de eerstgegeven lijn AB, dan wordt deze volgens de gulden snede gedeeld. Met andere woorden: AB verhoudt zich tot AC als AC tot CB. Er is dus evenredigheid van de deelen onderling en het geheel, zoals Vitruvius het uitdrukte.

De deelen die de lijn AB samenstellen noemt men gewoonlijk 'Major' (AC) en 'minor' (CB) of duidt ze aan met M en m.

De verhoudingen van den zooeven genoemden Egyptischen driehoek worden uit deze constructie gevonden door uit het punt P een loodlijn neer te laten op AB.
De verwantschap van de gulden snede met het kwadraat is duidelijk, zij wordt uit een half vierkant geconstrueerd; wij zien het verband ook bij de constructie van den gulden rechthoek (afb. 9). In een vierkant ABCD verbindt men het middelpunt O der grondlijn (DC) met het hoekpunt A of B. Met O als middelpunt en OB als straal beschrijft men een cirkelboog BE.


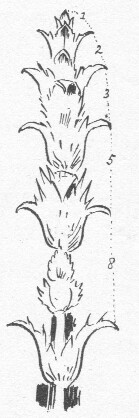
afb. 10 De reeks van Lamé
bij de bereklauw (Acanthus).
Waar deze de verlengde grondlijn (DC) snijdt (E) richt men een loodlijn op (EG) even hoog als de zijden van het oorspronkelijke vierkant. (20) Van den aldus verkregen rechthoek AGED verhouden zich de zijden volgens de gulden snede, in cijfers 1 : 1,618.

Die onmeetbare verhouding, 1 : 1,618.033.988.75 is voor gewone toepassing tot 1 : 1,6 te vereenvoudigen; het is deze gulden snede, die (aldus Delaruelle) Euclides en Plato als 'de' snede, d.w.z. de snede par excellence aangeduid wordt.
Men vindt deze verhouding ook in de z.g. reeks van Fibonacci of reeks van Lamé:
1-2-3-5-8-13-21-34-55-89-144 enz. waarbij elk getal uit de som van de beide voorafgaande bestaat. (21)

Nu treft men deze reeks zoowel als den gulden rechthoek in de natuur aan; de eivorm past in de laatste, in planten als de bereklauw (Acanthus, afb. 10) is de eerste terug te vinden. Fibonacci (Leonardo van Pisa) vond deze reeks in 1202, de verhouding wordt zuiverder gegeven naarmate de reeks voortschrijdt.

In de regelmatige lichamen van Plato reeds kristalliseerde zich het menschelijke denken in dit verband ook in driedimensionale vormen. Eén hiervan is ieder welbekend, al was het maar door het cubisme in de moderne schilderkunst: (22) de kubus, en wie moest hem niet, dit onverbiddelijk regelmatige lichaam, tot zijn wanhoop, teekenen op de school uit den tijd van onze jeugd!
terug naar de Inhoud

Regelmatige veelhoeken

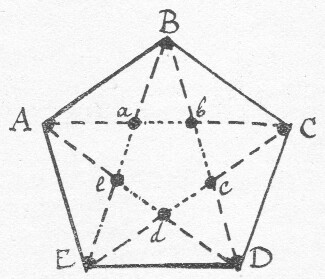
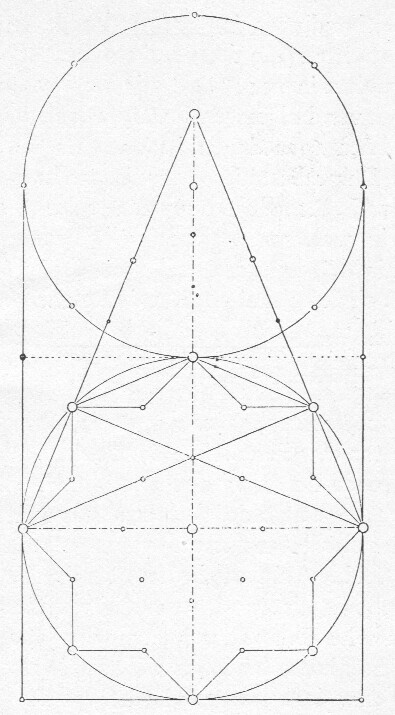
afb. 11 De regelmatige vijfhoek,
waarvan de diagonalen elkaar
volgens de gulden snede snijden.
Een ander van Plato's regelmatige lichamen is in verband met de gulden snede van belang: het regelmatig twaalfvlak, waarvan de zijden niet, als bij den kubus, vierkanten, maar vijfhoeken zijn.
In den regelmatigen vijfhoek nu ligt de gulden snede besloten (afb. 11). Trekt men namelijk hierin de diagonalen, dan verdeelen deze elkander volgens de gulden snede, terwijl door die snijpunten een nieuwe vijfhoek wordt gevormd, waarin ook weer de diagonalen elkaar aldus snijden en opnieuw een vijfhoek vormen, enzoovoorts tot in het oneindige. (23) Vandaar, dat de Duitschers spreken van de 'stetige Teilung'.

Uit de verbinding van de hoekpunten van de eerste en de tweede vijfhoek (Aa - Bb - Cc enz.) ontstaat de vijfpuntige ster of 'pentagram'. Bekend is, dat men vroeger aan dien vijfhoek goddelijke of tooverkracht toeschreef;

een toespeling daarop vindt men in Goethe's 'Faust' als Mephisto zegt dat dit teeken, ook 'druïdenvoet' genaamd, hem den weg verspert: (24)

,,Gesteh' ich 's nur! dass ich hinausspaziere
Verbietet mir ein kleines Hindernis,
Der Drudenfuss auf Eurer Schwelle..."
en Faust vraagt:
,,Das Pentagramma macht dir Pein?"


afb. 12 Een 'gulden passer', die de verhoudingen der gulden snede
aanwijst, gevonden te Pompei (Museo nazionale, Napels). In elken stand
geven de beide openingen de verhoudingen van major en minor (M en m).
De gedachte die wij hier ontmoeten is verwant aan die betreffende het teeken des kruises, dat een het (den!) Booze werende macht zou bezitten. (25) Wie het letterlijk opvat, zal zich door sommigen als bijgeloovig beschouwd zien, wie het figuurlijk opvat, zal in het opwekken van een zeker godsbesef toch ook het opwerpen van een slagboom tegen het kwade kunnen zien.
Maar hoe dan ook: hier ontmoeten wij het pentagram, dat de gulden snede bevat, als een goddelijk symbool; dit en het kruis zijn dat eeuwen lang geweest.

Nu zou ons hedendaagsch cynisme dezen gedachtengang, met pentagram, gulden snede, Plato, Euclides, Vitruvius, Da Vinci, Dürer, en alle eindeloos-terugvormende vijfhoeken gemakkelijker ter zijde kunnen schuiven, als niet allerlei geleerden de verhoudingen der gulden snede in allerlei kunstgewrochten en in de natuur, met den passer in de hand, hadden aangewezen.

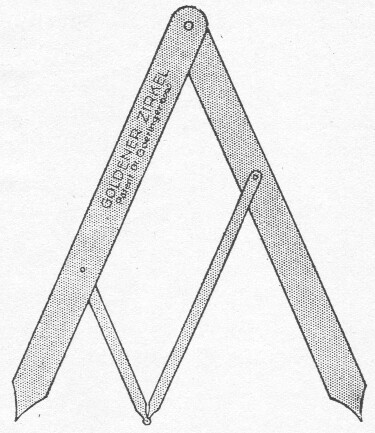
afb. 13 Passer van Dr. Goeringer
die de gulden verhouding aanwijst.
Hadden de Romeinen reeds hun 'gulden passer', die de verhoudingen der gulden snede aanwijst, in de negentiende eeuw kwam Dr. Goeringer met een passer, die het mogelijk maakt in een ommezien van eenig voorwerp na te meten, of de antieke verhouding er in besloten ligt, of niet (afb. 13).

Dit nu heeft ten gevolge gehad, dat in de baars en in de gazelle (afb. 14), in bloemen, kristallen en bladen van boomen en planten, en ten slotte ook in het menschelijke lichaam de gulden verhouding vele malen gevonden werd. In de knokkels van de vingers, in de verhoudingen van 's menschen hand, in boven- en benedenarm, in hals- en hoofdbreedte en waar niet al (27) vond men de 'sectio aurea', de gulden verhouding, terug.

Het valt iemand, die tracht onbevooroordeeld af te wegen, welke zin verhoudingstelsels nu eigenlijk hebben, soms moeilijk ernstig te blijven, zoowel bij het lezen van wat voor- als tegenstanders te berde brengen.

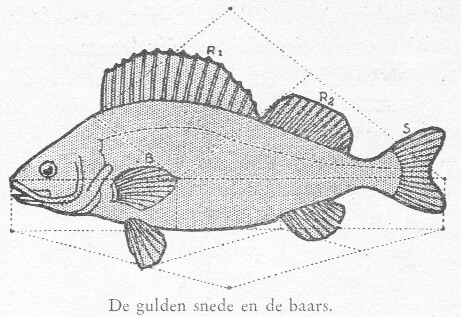
afb. 14 gulden snede en de baars
Wie denken mocht dat er geen magische werking van zulke verhoudingen zou uitgaan, wende zich tot Dr. Ernst Möckel; hij is een dergenen die schema's in de werken van Albrecht Dürer aantoont, terwijl hij er bij vertelt, dat Dürer zich bij zijn compositie niet van het aangegeven schema bediende, maar dat men het er hineininterpretieren kan.
Klaarblijkelijk kan men dus zoodanig door schema's en verhoudingen worden bezeten, dat men ze ziet waar ze volgens de zieners zelf niet zijn; sterker nog: men kan daarop weer promoveeren; Möckel verrichtte dit kunststukje. Dat hij nu waarlijk ook nog 'Ernst' moest heeten.


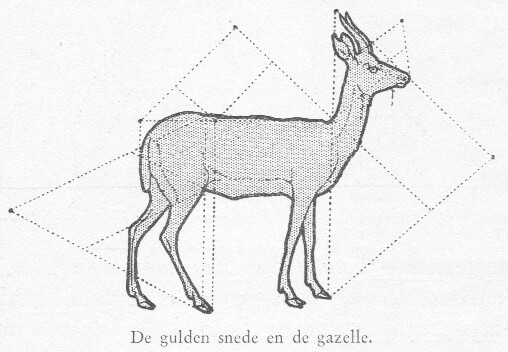
afb. 14 gulden snede en de gazelle
Dat de gulden snede in de natuur als tastbaar en eeuwig element aanwezig is en ook het zuiver mathematische denken van groote geesten als Plato en Euclides tot deze verhoudingen heeft gevoerd, liet niet na om vroeger en nu op velen een diepen, overweldigenden indruk te maken. Men zag er een goddelijke kern in, een regel die evenzeer het geschapene als het (28) abstracte, mathematische denken doorstraalde.
Men herinnerde zich Plato's uitspraak, dat de Godheid steeds mathematisch te werk ging; zoo werd het meetkundige een sleutel tot het goddelijke, een weg van den hemel naar de aarde scheen zich af te teekenen (en men vergat, dat ook andere verhoudingen in de natuur terug te vinden zijn).
terug naar de Inhoud

De menselijke maat
Maar hiernaast staat een andere gedachtengang, die een weg van de aarde naar den hemel scheen te bouwen. Voor al het menschelijke doen en laten, geldt allereerst het menschelijke zelf als uitgangspunt. Op het tempo, waarin wij ons van nature voortbewegen, d.w.z. van het normale loopen, berusten onze begrippen omtrent 'vlug' en 'langzaam'; in de muziek is het voortgaan, andare, de maatstaf voor een tempo dat met 'andante' een rustig voortschrijden aangeeft; zoowel het snelle als het langzame worden van hier uit bepaald. Evenzeer berust het op de afmetingen van ons lichaam, of wij andere schepselen 'groot' of 'klein' noemen.

Ten opzichte van het heelal is er niet zulk een groot of klein, volgens Hamlet is er zelfs geen goed en geen kwaad en maakt onze verbeelding het maar zoo. Wie dit niet kan beamen zal toch toegeven, dat de olifant, dien wij groot noemen, omdat wij onbewust met onszelf meten, tegenover het heelal, en zelfs tegenover de aarde zeer klein is, moeten toegeven, dat zelfs de aarde van het (29) heelal uit beschouwd, zeer, zeer klein moet heeten. Hoewel een mug, vergeleken bij een bacterie, enorm groot is, noemen wij hem klein, ofschoon een toren vergeleken bij den hemel laag is, noemen wij hem hoog. Wij meten met onszelf, zij het vaak onbewust.

Zo gaan tevens onze concepties omtrent welgemaaktheid uit van het menschelijke lichaam; ook al zijn wij ons daarvan evenmin bewust als bij het benoemen van afmetingen, snelheden of het goddelijke. Zooals ons lichaam gewoonlijk gebouwd is, zo vinden wij het redelijk en schoon. Een dwerg of een waterhoofd vinden wij niet mooi en de proporties van een apenlichaam dat op de menschelijke gestalte lijkt maar er duidelijk van afwijkt, vinden wij minder fraai dan die van den mensch; "Je lijkt wel een aap" is een opmerking, die geen sterveling als een compliment zal beschouwen.

Of die opvatting nu juist is of niet, kan hier buiten beschouwing blijven, hier worde alleen geconstateerd, dat de algemeene gedachtengang den aap als minder fraai dan den mensch rangschikt. Spraken wij op de voorafgaande bladzijden van het goddelijk element, dat in de gulden snede, het menschelijke denken en de menschelijke gestalte wordt gevonden, in dezen tweeden gedachtengang treedt niet het goddelijke maar het menschelijke element op den voorgrond. (50)

Dit heeft ten gevolge dat het den mensch redelijk voorkomt, dat de proporties van het menschelijke lichaam goede proporties zouden zijn voor die producten van bouwkunst en kunstnijverheid, welke door hun gebruik met het leven van den mensch verbonden zijn. (51)
Zij, en zij alleen, zijn redelijke maatstaven voor de afmetingen van deur of stoel en de voorwerpen die wij hanteeren; in hun onderdeelen paste men de verhoudingen der gulden snede vaak toe. Was de eerste gedachtengang er dus een van openbaring van goddelijke werkzaamheid in het geschapene, de tweede zoekt naar harmonie van den mensch uit. Zulk een harmonie vindt men in een Griekschen tempel, maar niet in een fabriek of fabrieksschoorsteen, om het nut aldus gevormd, zoowel in afmeting als proportie zijn zij in het algemeen 'on-menschelijk'.

afb. 15 Portret van Fra Luca Pacioli
door Jacopo de' Barbari (1450-1515).
Aan Pacioli's linkerhand
het regelmatige twaalfvlak.
Michelangelo heeft gezegd, dat alleen hij een goed architect kan zijn, die het teekenen van des menschen gestalte volkomen beheerst. Hij zal hiermede wel niet bedoeld hebben, dat men de maten van armen en beenen op gevels moet gaan afpassen, maar waarschijnlijk wel, dat goede architectuur een even harmonische uitgewogenheid en aan haar bestemming en gebruik beantwoordende bouw moest bezitten, als die welke het menschelijke lichaam eigen is.
Als bij het toekennen van krachten aan het pentagram, zal hier de figuurlijke beteekenis boven de letterlijke gesteld moeten worden, maar hoe dan ook: hier wordt eens te meer van den mensch uitgegaan. Men kan zelfs meenen dat het Westersche denken zoo van mensch-vervuldheid vol staat, (32) dat het zich het goddelijke steeds als de perfectie van het menschelijke heeft voorgesteld en dat dit verschijnsel zich in het abstracte, onze religieuze concepties, evenzeer voordoet als bij de Grieksche godenbeelden in het concrete.
terug naar de Inhoud

Luca Pacioli - De Divina Proportione

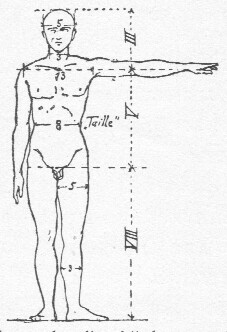
afb. 16 De gulden verhouding
bij den mensch. Hoogtematen:
III, V, VIII. Breedtematen: 3-5-8.
Het goddelijke element der gulden snede werd wel het sterkst door Fra Luca Pacioli onderstreept, toen deze in 1509 te Venetië zijn 'De Divina Proportione', Over de 'goddelijke' deelverhouding, liet verschijnen en waarin hij voor het eerst van 'sectio divina' spreekt.
Ook de sterrekundige Kepler geeft haar die benaming in zijn 'Mysterium cosmographicum de admirabili proportione orbium coelestinm' van 1596. Pacioli's portret werd door een zijner leerlingen, den bekenden Jacopo de' Barbari, geschilderd (afb. 15); men ziet hem er de wiskunde onderwijzen, den bijkans fanatieken Godzoeker, als een toovenaar met attributen en het regelmatig twaalfvlak met zijn wonderbaarlijke vijfhoeken, die de gulden snede omsluiten, is daarbij niet vergeten.

Ook latere eeuwen hebben even felle verdedigers van de gulden snede voortgebracht.
Zeising geeft in het midden der 19e eeuw als gemiddelde van 2000 metingen van de menschelijke gestalte:

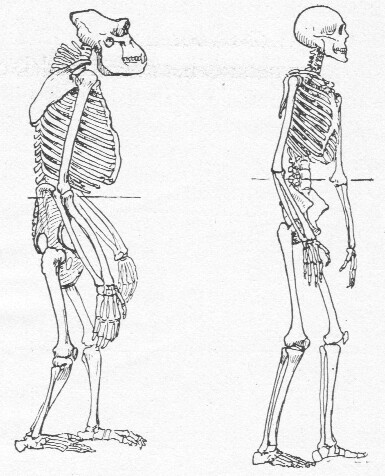
afb. 17 Gorilla: het middel ligt op
het midden der lichaamshoogte;
mensch: op 5/8 der lichaamshoogte.
hoogte van den oogappel 5,1
hoogte van de neusvleugel 8,1
hoogte van oog tot wenkbrauw 13,1
afstand van mond tot kin 21,2
afstand van oog tot haarinplanting 34,4
afstand van oog tot kruin 55,7
kruin tot basis van den neus 90,1
afstand van keel tot kruin 145,8
afstand van knie tot voetzool 236,0

en zeker is de overeenkomst met de reeks van Fibonacci treffend: 5-8-13-21-34-55-89-144-233, maar de willekeur der volgorde, of liever de opzet om overeenstemming te verkrijgen en de vaagheid der meetpunten is dat niet minder.

Pfeifer toont de gulden verhoudingen in 's menschen gestalte aan op de wijze die de bovenstaande afb. laat zien (afb. 16). (34) De lijn, die men door de taille en de ellebogen kan trekken, verdeelt de totale lichaamshoogte in deelen, die zich verhouden als 3 en 5.

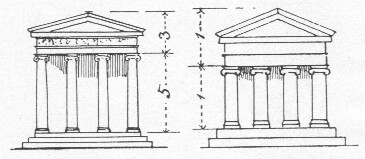
afb. 18 Gorilla, mensch, Grieksche tempel.
Het midden ligt dus belangrijk lager dan de taille, het ligt in het heupgewricht. Dit geeft den mensch een grootere rijzigheid van gedaante dan den gorilla: (35) daar ligt de taille wel in het midden der hoogte van de geheele gestalte (afb. 17). De schrijver gaat dan na of de Grieksche tempel mensch-achtig of aap-achtig geproportionneerd is en teekent ons voor hoe ze zou zijn als de zuilen tot de halve hoogte, het apen-middel, of tot vijf achtste, de menschentaille, reiken. Ongetwijfeld geeft iedereen aan dit laatste, de gulden verhouding 3-5, de voorkeur (afb. 18).

afb. 19 Griekse amphora van
± 300 v.Chr. waarin de gulden
verhouding is aan te wijzen.

terug naar de Inhoud

Bewuste of onbewuste toepassing
De vraag doet zich nu voor: pasten de Grieken de verhoudingen der gulden snede bewust of onbewust toe? Van de Romeinen weet men het zeker, maar ook de veelvuldigheid, waarmede men in Grieksche kunst de zoo geroemde proporties kan aanwijzen, maakt het bijna zeker dat hier van bewuste toepassing sprake moet zijn.
Wie de hier afgebeelde amphora (afb. 19) van ongeveer 360 v.Chr. met Goeringer's passer nameet, bevindt het volgende. (36) De grootste en de kleinste breedte van het 'vat', dus de buik met de bocht naar buiten en de hals met de bocht naar binnen, verhouden zich als major en minor. Hals en 'vat' worden ter hoogte van de aanhechting der ooren gescheiden door een z.g. 'eierlijst'. Deze nu blijkt de totale hoogte eveneens in major en minor te verdeelen. Verder is de hals, zonder ooren, weer minor tegenover den afstand tusschen de genoemde eierlijst en den onderkant van den meander, de 'Grieksche rand'. En hetgeen onder dien meander ligt, dus het onderste deel van het 'vat' en de voet, is opnieuw in major en minor verdeeld.

afb. 20 Stradivarius viool, 1701
Hier is zelfs de cynicus geneigd, van bewuste 'analogia': verwantschap der onderdeelen, te spreken; dit alles kan maar niet toevallig zijn. Merken wij overigens op, dat er vele Grieksche vazen zijn waarbij men haar ook vele malen vindt, en andere waarbij men tevergeefs de bedoelde verhouding zoekt, op het eerste gezicht althans.
terug naar de Inhoud

Vioolbouw
Hoe moeilijk op dit gebied conclusies te trekken vallen, zien wij bij de viool (afb. 20). Hier weten wij nu buiten kijf, dat de vioolbouwers, heden nog, met de verhoudingen der gulden snede werken en zoo tot de gedaante van dat allerprachtigste instrument komen. Met den passer van Goeringer gewapend, toog schrijver dezes er op uit om een Stradivarius na te meten. Het resultaat geeft de afbeelding te zien (afb. 21). Maar toen hij het resultaat aan een vioolbouwer toonde, was het eerste wat deze zeide: "Ja, maar zoo is het niet." (38)

Hierin ligt dus zoowel een waarschuwing om voorzichtig te zijn ten aanzien van gemakkelijk in violen, baarzen of gebouwen gevonden gulden verhoudingen: zij behoeven nog niet de constructie te onthullen (wij noemden in dit verband reeds Ernst Möckel), al geven zij een aanwijzing dat de gulden verhouding klaarblijkelijk intuïtief of uit stijlgevoel wordt toegepast. Immers, berusten de hoofdzaken van het viool-lichaam er op, dan zal men uit stijlgevoel allicht de krul en de voluut ervan eveneens de bedoelde verhouding geven: analogia, zeiden de Grieken. Analogie.


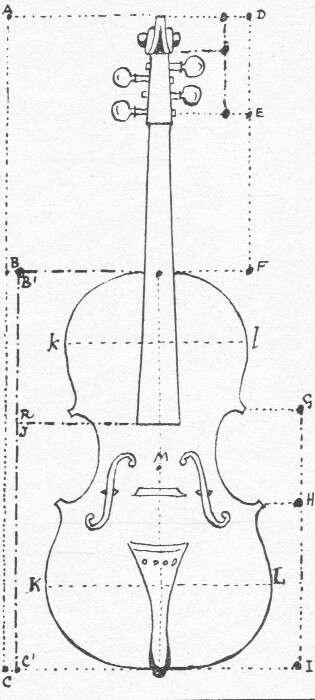
afb. 21 Gulden snede verhoudingen
in de Stradivarius aangetroffen.
Bij de viool is echter niet de uitwendige gedaante, maar de door het hout omsloten ledige ruimte essentieel: dit is het klinkende element. Reeds Lao-tze verklaarde dat een beker meer de ingesloten ruimte dan het tastbare lichaam is en zeker geldt dat hier. Stradivarius bouwde zijn instrument om een vorm heen gelijk de schoenmaker de schoen vormt om een leest. Het is hierom dat de inwendige vorm volgens de gulden snede wordt geconstrueerd (afb. 22).
Max Möckel bouwt den uitwendigen vorm op uit regelmatige vijfhoeken. Adolf Beck en Paul Gerhard Schmidt doen het den inwendigen uit het halve vierkant der gulden snede.

Bij het vastleggen der punten 1, 2, 3, 4 en 5 (respectievelijk 1*, 2*, 3*, 4* en 5*) is uitgegaan van de volgende verhoudingen:
CM : DM = AD = DB
CM : GM = GM : GC
DM : G*M = G*M : G*D
GM : HM = G*M = H*M
BC : FC = FC : BF
FF* L DC

FF* is de lijn waarop de kam staat en de kurven der F-gaten liggen.
MK = LM
LK = L*K
L*O = L*K = 1/2 (L*L)
OL : SL = SL : OS

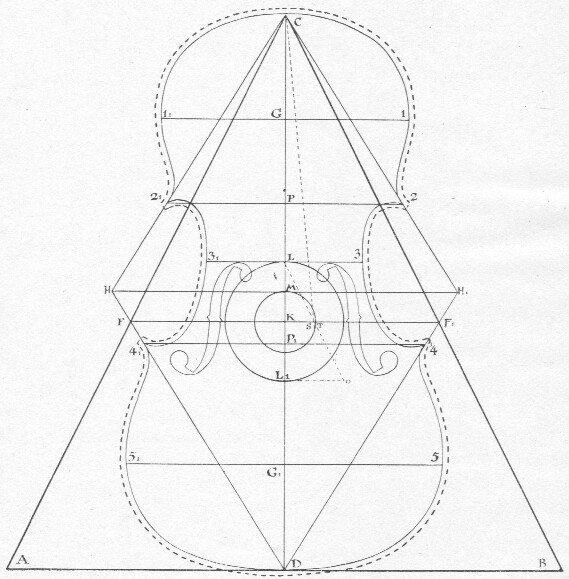
afb. 22 Geometrische verhoudingen
als grondslag van den vioolvorm
(in aansluiting aan de constructie-
methode van A. Beck,
Düsseldorf, Paul Gerhard Schmidt).
S* geeft de plaats aan van de stapel (steun voor het bovenblad).
CS t 5 - 5 (grootste breedte van het onderdeel)
DK = 1 - 1 (grootste breedte van het bovendeel)
1/2 (CS) : (5 - 5*) = 3 - 3* (de kleinste breedte van de viool).

KC : PC = PC : KP
2 - 2* | CD (snijpunt P)
PD : P*D = P*D : PP*
4 - 4* | CD (snijpunt P*) (43)

Er zijn wel eens theoretici die de gulden snede maken waar ze niet is en den vioolvorm persen in verhoudingen die hij in werkelijkheid volstrekt niet bezit: wij nemen zulk een voorbeeld hier over uit een boekje waar een misbaksel 'viool' heet (Th. Wolff, De gulden snede) (afb. 23).

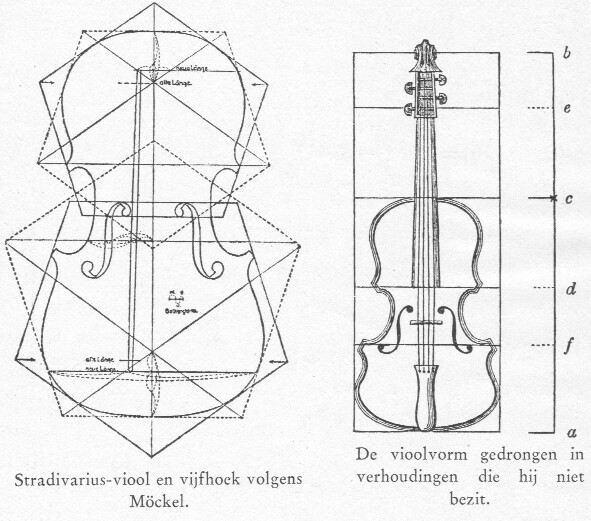
afb. 23 Stradivarius-viool en
vijfhoek volgens Möckel
De vioolvorm gedrongen in
verhoudingen die hij niet bezit.
Zij, die de mystieke waarde van antieke schema's gaarne naar voren brengen, zoeken deze ook wel eens waar zij niet te vinden zijn. Prof. Dr. H.A. Naber schrijft in zijn 'Meetkunde en Mystiek' heel eerlijk en vermakelijk, hoe hij in de jubileum-zegels, door den (44) architect De Bazel ontworpen, ook een wiskundig systeem meende te zien en den ontwerper daarnaar vragende het ontnuchterende antwoord kreeg, dat geen andere beperkingen in acht genomen waren dan die der... perforeermachine.

Het blijft niettemin de vraag, in hoever in schijnbaar zelfstandig bedachte ontwerpen ondergrondsch, onbewust, oude verhoudingen doorwerken. Een onzer bekendste grafische ontwerpers, die schrijver dezes de gulden snede 'een ezelsbruggetje' noemde voor menschen zonder rhythmegevoel, verklaarde zijn ontwerp voor een drukletter 'vrij' te hebben gemaakt; het later nametende, bleek het in de verhoudingen der gulden snede te passen...

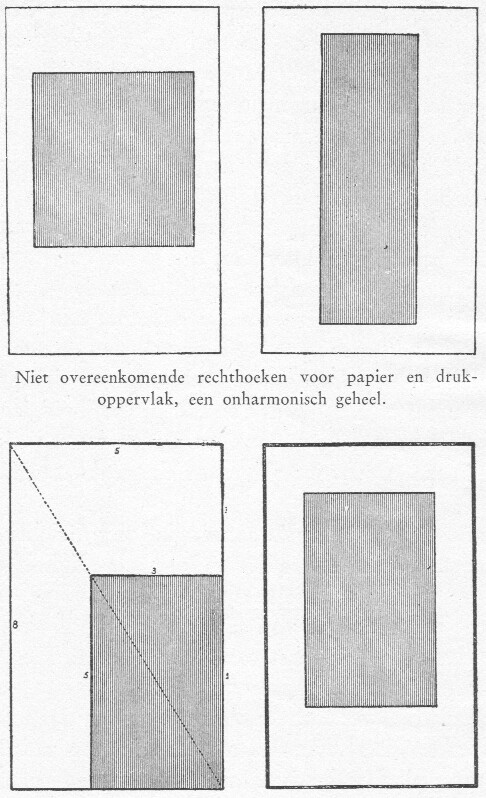
afb. 24 Boven: rechthoeken
voor papieren drukoppervlak
niet overeenkomend: onharmonisch.
Beneden: papier en drukoppervlak
op een los blad in overeenstemming
gebracht m.b.v. den diagonaal.
Waar is dan die vrijheid en wat is dan rhythme-gevoel, zou men willen vragen? Is dan in zulk een geval niet onbewust de gulden snede toegepast?
terug naar de Inhoud

Papiermaten
Dat evenredigheid, de 'analogia' der Grieken, ons aesthetische gevoel bevredigt en onevenredigheid niet, valt het gemakkelijkst te zien bij eenvoudige rechthoeken: een bladzijde van een boek en het drukoppervlak, dat door den tekst wordt ingenomen. Heeft het blad papier een gedaante overeenkomstig den gulden rechthoek, dan voldoet een drukoppervlak dat een zuiver vierkant is al evenmin als een, dat een zeer langwerpige gedaante bezit. (45) Men vindt overeenstemming met behulp van den diagonaal en de gulden verhoudingen: 3 : 5 voor het bedrukte oppervlak en 5 : 8 voor het blad papier (afb. 24).

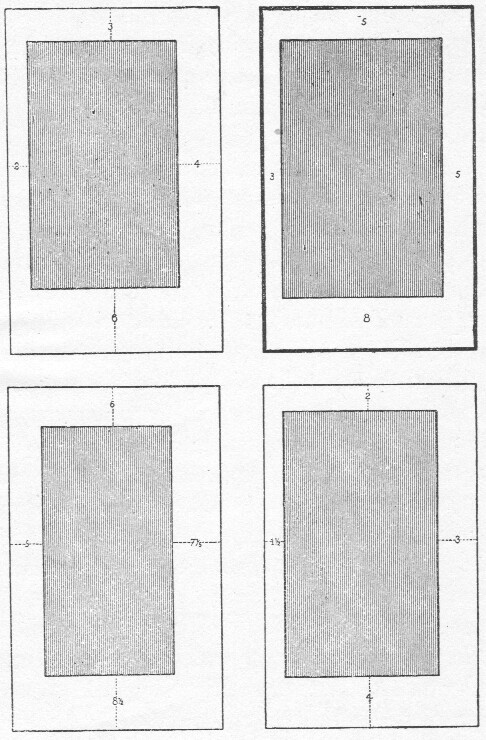
Bij een dubbele pagina wordt bijv. in den rug van het boek, zoowel voor de linker- als rechterbladzijde, 3 genomen, boven en aan de buitenzijde 5, onderaan 8. Dit althans is een verhouding die men vaak aantreft en die ons schoonheidsgevoel bevredigt (afb. 25).

Variaties daarop zullen ons aanvaardbaarder lijken dan de onharmonieerende rechthoeken van blz. 46 boven; op blz. 49 is een oud boek links boven weergegeven (afb. 26), een volgens de gulden snede rechts boven; een druk van William Morris, links onder; een indeeling van Edward Johnston rechts onder; al deze voldoen ons beter dan indeelingen als op blz. 46 bovenaan.


afb. 25 Boven: de bepaling der
marges voor een rechtsche
boekpagina volgens de gulden
snede en de diagonaal.
Marges 3:5:8
Beneden: een dubbele pagina.
In toegepaste kunst, als het bepalen van boekformaten en drukoppervlakken, spreken de factoren niet mede, die de vrije schepping eens kunstenaars bovenal dragen. Het is dan ook begrijpelijk dat drukkers door de eeuwen heen de gulden evenredigheid hebben toegepast. Een der om zijn schoonheid beroemdste drukwerken ter wereld is Manutius' 'Poliphilus' van 1499; het is op dit formaat gedrukt. Het papier, waarop deze regels geschreven werden, is van een alledaagsch schrijfblok; het meet 21 x 26 cm., d.w.z. dubbelgevouwen is het 13 x 21 cm., de gulden snede. (48)

En dat is met vele z.g. 'kwarto' boekformaten het geval, 'octavo's' als Ten Bruggencate's woordenboek; het zak-notitieboekje, blijken, als de briefkaart, het visitekaartje en het lucifer-doosje onzer dagen alle aan de gulden verhouding te beantwoorden.

Toen nog onlangs de Haagsche kunstkring een merkteeken zocht, ontwierp men er een dat de vijfpuntige ster der gulden snede, het pentagram, in den cirkel, ingeschreven in een vierkant, te zien geeft. Men berichtte den leden, wat voortaan het kenteeken van den Haagschen Kunstkring zijn zou: Het 'penta- gramma dissimulatum', de binnen den vijfhoek met de verhoudingen der 'sectio divina' geteekende vijf-puntige ster.

afb. 26 Ruimteverdeling volgens
de gulden snede (rechts boven)
en welstandige varianten daarop.
Deze heeft als kern de malve (Malva Campestris), welke reeds den Pythagoreeërs heilig was, omdat de bloem zich naar de zon toekeert. De vijf, den Haagschen kunstkring vormende groepen (bedoeld zijn de muziek, beeldende, bouw- en tooneelkunst en de kunstlievenden) omringen het symbool, dat in de kunst op zoo talrijke wijzen met gewijde schoonheid verbonden is."

Tot op den huidigen dag heeft de gulden verhouding zich dus gehandhaafd, al was zij minstens eenige eeuwen oud toen onze jaartelling begon. Zij heeft vele ernstige en sommige over enthousiaste aanhangers gevonden, maar ook tegenstanders, die haar eenvoudig verwerpen. (50) Vindt Pacioli haar de 'goddelijke' verhouding, passen Grieken en vioolbouwers als Stradivarius haar toe, lijnrecht hier tegenover staat de afwijzende houding van anderen. In het 'Architectonisches Wörterbuch' van Müller und Matthes wordt de gulden snede allesbehalve als goddelijk betiteld, zij heet daar: dikwijls in vollen ernst aanbevolen nonsens, ,,ein oft sehr ernst empfohlenen Blödsinn". Hoe die tegenstelling te verklaren?

afb. 27 Dürer's
randversiering van het
gebedenboek van Keizer
Maximiliaan. Tekst en rand in
analogia, beide toepassingen
van de gulden snede.
Gaan wij na waar de gulden snede bewust wel en bewust niet is toegepast, dan helpt ons dat misschien op weg. Vergoddelijking van vereerders, verguizing van tegenstanders brengt geen bouwstoffen aan; deze volstaan gewoonlijk met termen als 'Blödsinn', bijgeloof, verouderd ezelsbruggetje, - hetgeen op zichzelf heel wel juist kan zijn; dergelijke uitlatingen echter maken ons niet duidelijk waarom de gulden snede dan eeuwenlang, zelfs een paar duizend jaar, vat op 's menschen geest had. Gevallen, waarin zij werd toegepast of gemeden, en ook de argumentatie van haar vereerders, kunnen ons bij het zoeken naar een antwoord te pas komen. Bezien wij er enkele nader.

Papierformaten, zoo zagen wij, hadden vaak de gulden proporties. (51) Nu heeft men de laatste jaren onze gebruikelijke papierformaten willen wijzigen, standaardiseeren. De geestelijke vader van dit streven is de bekende theoreticus Prof. Ostwald. Hij ontwierp een stel formaten, die gegrond zijn op de eenige maat, welke bij halveering opnieuw dezelfde maatverhouding van het geheel bezit. Het is de verhouding welke men aantreft tusschen de zijde van een kwadraat en zijn diagonaal, 1 : √2 ofwel 1 : 1,4142. Van dezen grondslag uitgaande stelde men een A-reeks, B-reeks, C-reeks en D-reeks samen.

afb. 28 De gulden snede in de
Gothiek: de Munster te Freiburg
(volgens Pfeifer)
Het aldus ontstane 'normale' formaat briefpapier 44 (210 x 297 m.m.) houdt het midden tusschen z.g. folio-schijf (210 x 330 m.m.) en het z.g. kwarto-post (220 x 280 m.m.). Men gaat hier uit van nuttigheids-overwegingen: de officieele toelichting voegt aan het vorenstaande toe, dat de nuttige ruimte belangrijk grooter is dan van het kwarto-post. Het eerste formaat van de A-reeks, A0, heeft een oppervlak van een vierkante meter (841 x 1189). Alles berust hier op zakelijkheid. Op nut. Niet op eenig gevoel.

Maar deze formaten winnen slechts langzaam terrein van de oude, die op de aesthetica, het meestal onbe- wuste schoonheidsgevoel gegrond zijn. De maten van oude papiersoorten hangen geheel af van den schepbak, en toen de maker hiervan zijn kunstnijverheids-product schiep, sprak daarin zijn gevoel voor proporties bij intuïtie mede. (52) Dit gevoel, dat bij anderen weerklank kan vinden, ontbreekt ten eenen male bij de 'normaal-formaten'; zij bevredigen daarom den aesthetischen zin niet.
Sommigen, die geen aesthetischen zin hebben; bemerken daar niets van en gebruiken de normaal-formaten. Is hier nu sprake van aesthetischen zin, of alleen maar sleur, vasthoudendheid? Toen dezelfde Prof. Oostwald een reeks publicaties liet verschijnen en daarvoor het nieuwe 'Weltformat' no. IX koos, werd het bedrukte oppervlak, de 'zetspiegel', precies... volgens de verhoudingen der gulden snede genomen, zooals Rud. Engel-Hardt niet zonder spot opmerkt, want het ,'Weltformat' wilde nu juist opruiming hou- den onder de oude formaten. ,,Man darf hieraus schliessen, dass entweder dem Autor, dem Verleger oder dem Drucker, vielleicht auch allen zusammen, ein dem Weltformat angepasstes Satzformat (drukopper- vlak) ästhetisch so wenig befriedigend erschien, dass man zum Goldenen Schnitt griff und dafür lieber unschöne, ja geradezu unmögliche Papierränder mit in den Kauf nahm."


afb. 29 De gulden snede in de
Renaissance: de Certosa, Pavia
(volgens Pfeifer)
Van oudsher was het bij het boek namelijk gebruik, dat men de plaatsing van den zetspiegel zoodanig koos, dat de marges ongeveer tot elkaar stonden als 3, 5 en 8, en wel zoodanig, dat het 'rugwit', de marge die langs den rug van het boek loopt, het eerste cijfer, (53) de 'kop', de bovenzijde, de 5 krijgt en onderaan het z.g. 'staartwit' 8 als breedte heeft. Men gaat daarbij uit van de overweging, dat bij een opengeslagen boek de twee bladzijden, die men voor zich heeft, een geheel vormen; zooals William Morris zeide, is de eenheid, waaruit een boek is opgebouwd, geen afzonderlijke losse bladzijde, doch een paar: de linker en rechter samen. Omdat deze dus bij elkaar behooren, moet de rugmarge smal zijn: de drukoppervlakken behooren voor het lezend oog bij elkaar.
Om dezelfde reden zullen de buitenmarges, die het leesoppervlak van de rest van de wereld afscheiden, en welke dus als het ware den lees-achtergrond vormen, grooter breedte vragen. De grootste van deze drie eischen buiten- en onderkant, omdat men deze rnarges tevens gebruikt om het boek bij het lezen vast te houden. De onderkant zal van deze weer de breedste moeten zijn, omdat ons oog zoo gebouwd is, dat het optisch midden boven het mathematisch midden ligt; m.a.w. wij zien het midden hooger dan het is. Het bedrukte gedeelte zou ons anders op het veld eener bladzijde afgezakt toeschijnen.


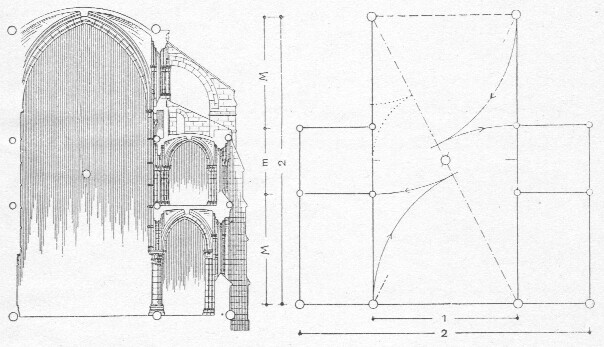
afb. 30 De gulden snede in de
Gothiek: De kathedraal van Laon.
De deelpunten worden met de
gulden snede gevonden.
Van al die fijne, kunstzinnige uitgewogenheid, die nog weer beïnvloed wordt door het lichter of krach- tiger zwart der bladzijde, dat afhankelijk is van het gebruikte lettertype, van het wit tusschen de regels, en zoo meer, blijft dus al heel weinig over (54) als men een Weltformat en een gulden rechthoek dooreenhaspelt. Daar de drukkunst juist bestaat in het gevoelig afwegen van die zwart-en-wit verhoudingen, is het voor een goede drukker dan ook wel dwaas dat de man, die nieuwe proporties wilde scheppen in plaats van de oude, ze op zulk een onbeholpen wijze in praktijk brengt. Het is klaarblijkelijk gemakkelijker het oude te verwerpen dan te evenaren; hier werd het slechts half afgeschud onder den dwang eener redeneering zonder kunstgevoel.
Geheel verwierp het tijdschrift 'Wendingen' geijkte begrippen. Dit is er een voorbeeld van, dat het oude als verouderd aangevoeld en daarom verlaten werd. Men gaf 'Wendingen' den vorm van een vierkant, een zuiver kwadraat en componeerde een decoratieve vulling daarvan uit ornamentale, breede en smalle meander-achtige vormen, en den zetspiegel beide, die dan met de blanke gedeelten gezamenlijk een ornamentatie van dat vierkant waren. Deze 'moderne' zienswijze vond wel toepassing voor berichtkaarten en dergelijke, doch bleef voor het boek bij een enkele uitzondering, omdat het lezen zoo niet vergemakkelijkt, maar bemoeilijkt wordt. Het baanbrekend nieuwe van 'Wendingen' was door den architect Wijdeveld aan de architectuur ontleend; daar waren de oude maatstaven als ongeschikt voor onzen tijd, als knellend bevonden en verworpen. (55)


afb. 31 De kathedraal van Ferrara.
De gevel is opgebouwd uit drie
rechthoeken, die elk uit een half
kwadraat bestaan. De gulden snede
geeft de deelpunten.
In de beeldende kunsten, in de literatuur, waar oude versvormen verlaten werden, viel hetzelfde waar te nemen. Hier dus een zeer opzettelijk afwijken van de gulden snede op artistieke gronden (zooals trouwens bij 'Wendingen' het papier gevouwen en de afleveringen gebonden werden op een eveneens opzettelijk andere manier: imitatie Chineesch). Dit 'moderne' verouderde snel.
Daarentegen handhaaft de gulden verhouding zich op aflerlei gebieden, niet alleen op dat van de vioolbouw. Dat de sierlijke, zoo spontaan schijnende vorm van dit instrument uit de gulden snede of uit den vijfhoek geconstrueerd is, zal menigeen verbazen. Hebben de oude vioolbouwers onbewust deze vorm gekozen, dan blijft toch het feit der verhoudingen bestaan; bewust of onbewust, de gulden snede passen zij toe.
Een hedendaagsche vioolbouwer zeide schrijver dezes, pas 'vrij' te gaan werken nadat hij de gulden verhoudingen der viool goed in zijn geest had opgenomen. Dat 'vrij' wilde dus niet zeggen 'willekeurig', doch duidde slechts op variaties binnen gulden hoofd-proporties, na jarenlang op mathematischen grondslag gewerkt te hebben.


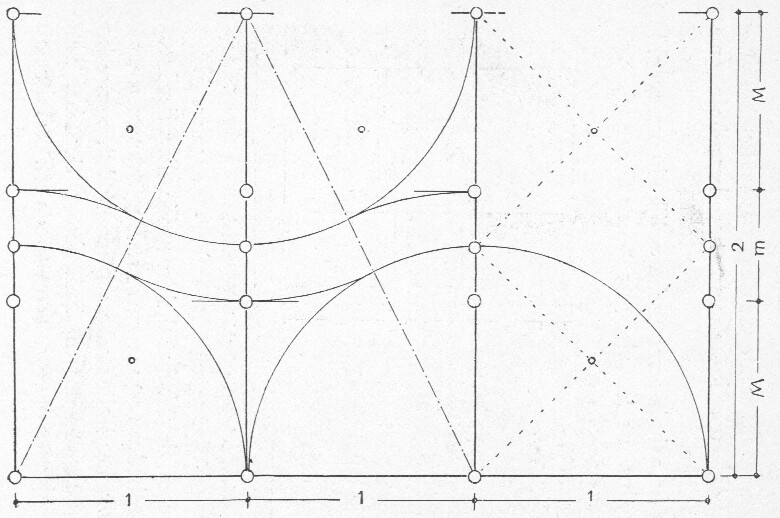
afb. 32 De deelpunten worden
volgens de constructie der gulden
snede gevonden (m: minor, M: major).
De gevel is driedelig; elk deel bestaat
uit het halve vierkant der gulden snede.
Nu doet zich bij de viool echter wel een bijzonder geval voor. Bij gebouwen, vazen en andere gebruiks- voorwerpen wisselt de vormgeving min of meer met den aard van het gebruik. (56) Bij het boek is dat al minder het geval, sedert de viool haar idealen vorm verkreeg, bleef het gebruik hetzelfde. Wel verandert in het algemeen in de kunstnijverheid de stijl der vormen wanneer die overwegend aesthetische beteekenis hebben, maar bij de viool is het niet in de eerste plaats om fraaie vormgeving, maar om de voortgebrachte klank en bespeelbaarheid te doen, en dit zijn constant-blijvende factoren. Men zal dus in den vioolbouw juist de hoofdvormen van een Stradivarius behouden en er slechts in subtiele kleinigheden van afwijken, terwijl men geen architect van 1700 op die wijze zal navolgen als men inplaats van het muziekinstrument een hedendaagsch gebouw behoeft, of een meubel.
Hieruit zou de conclusie volgen, dat het trouwblijven aan de gulden snede meer geldt naarmate de vormgeving gebondener is, en minder afwijking veroorlooft, zij het om redenen van hanteerbaarheid en practisch gebruik (het boek), zij het om redenen van ideëelen aard (de viool, al heeft de hanteerbaarheid ook hier invloed op den vorm).


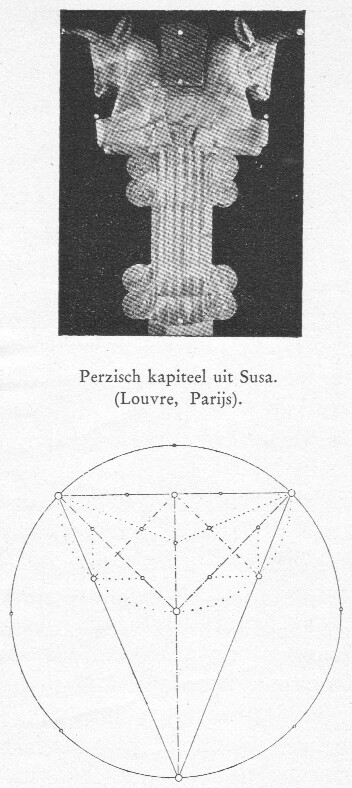
afb. 31 Persisch kapiteel uit Susa
(Louvre, Parijs)
afb. 32 De grondvorm is een driehoek,
uit den cirkel afgeleid door deling in
achten van den omtrek.
In de vrij-beeldende kunsten zou dan de beteekenis der gulden snede wéér beperkter moeten zijn. Men heeft er op gewezen, dat in tde theoretische geschriften van Dürer de gulden snede zelf niet wordt genoemd, terwijl hij deze bijv. wel toepaste (57) toen hij het Gebedenboek van Keizer Maximiliaan verluchtte: de tekst had zuiver de verhouding van 'major' tot 'minor', en hij gaf, in 'analogia' daarmede, die ook aan de omranding (afb. 27).
Maar met het zelfstandig-geschilderde schilderij wordt dit anders. Is er weinig tegen in te brengen als men betoogt, dat de proporties van een stoel aan die van het menschelijk lichaam moeten beantwoorden; bij beeldende kunst vallen zulke grondslagen weg, dan hebben maten en formaten een andere dan een welstandigheids-waarde, dan dienen zij alleen tot het uitdrukken van zielsaandoeningen van den maker. Het nut, het gebruik valt weg bij de 'vrije', beeldende kunst.

Overweegt in bouwkunst en kunstnijverheid het gebruik door anderen, in de vrij-beeldende kunst over- weegt de inventie van den maker. Overweegt in een periode of persoon het nijverheidsbesef, dan zal men de aesthetische begrippen daarvan ook willen overplanten op het terrein der vrije kunst. Een voorbeeld hiervan vinden wij bij Dürer, die in zijn schilderkunst de schoonheid van den mensch zocht te construeeren en daarin faalde, terwijl de constructieve grondslag aan zijn ornamentiek niet in den weg stond.

afb. 33 Assyrische relief uit het
paleis van Assurnasipal, Nimrud,
± 860 v. Chr.
afb. 34 De opbouw uit het
kwadraat en de verhouding van
de zijde en de diagonaal van het
kwadraat (1:√2).
(Staatliche Museen, Berlijn)
Leeft een gemeenschappelijke schoonheidsnorm in gansch een volk, zooals bij de Grieken ten tijde van Polykleitos, dan is het gansch iets anders; (59) dan is de canon geen nieuwbedachte constructie als die van Dürer, maar de belichaming van een gemeenschappelijk schoonheidsideaal. Hier staan wij voor het verschil tusschen gemeenschapskunst en persoonlijke inventie. Leeft een kunstideaal waarlijk in een volk, een periode, dan kan een formule een gemeenschappelijke grondslag zijn. Is dit ondergrondsch contact verloren gegaan bij den bovengrondschen uitgroei tot zelfstandige individuen, dan kan van eenige formule weinig meer uitgaan. Traditie wordt dan conventie, als men zich er niet van losmaakt.
Niet alleen Dürer vergiste zich echter; de schrijver Riegler wijst ons de gulden snede aan in een enkel schilderij van den Delftschen Vermeer, van Rembrandt, van Rafael, Funk-Hellet kan werken van Rafael, Veronese, da Vinci, Luini in den vijfhoek doen passen. Wordt hier niet vergeten dat één zoo'n kunst- stukje ten aanzien van het geheele oeuvre van die kunstenaars niets zegt, en dat het een ander geval geldt dan bij gebruikskunst als tempels of violen? Dat de schoonheid dezer kunstwerken er niet een is van enkel verhoudingen?

De menschheid vond steun in dergelijke grondslagen toen het onbewust-gemeenschappelijk kunstgevoel nog niet plaats gemaakt had voor het individueel-bewuste. Als artistiek dogma verloor de canon aan beteekenis naarmate het persoonlijke een eigen uiting zocht. (60) Het gemeenschappelijke kunstgevoel leefde sterk in onze Gothiek, zwakker in onze Renaissance (afb. 28-32): het individueele won veld ten koste van het hereditair-gemeenschappelijke.
terug naar de Inhoud

De traditie
Het hereditair-gemeenschappelijke kunstgevoel leeft eerst onbewust, later bewust. Bij de Oostersche volken kunnen wij de onbewustheidsperiode, die wij achter ons hebben, heden nog waarnemen. De Javaansche wajang en batik, het Balineesche snij- en beeldhouwwerk de weefkunst van Atjeh, Palembang, Soemba, Timor, Rotti, zij leven onbewust en vormen een deel der naïeve cultuur, men groeit er mede op als met de eigen taal, (63) elk eiland, elke landstreek heeft zijn eigen normen, die meer dan het aandeel van de weefster het artistiek resultaat bepalen. Zij zijn, vanzelfsprekend, leidraad, artistieke grammatica, als driehoek of gulden snede elders was.
Treedt eenmaal de persoonlijke vinding op, dan smeedt elk individu zich een eigen grammatica: wie de taal van Michelangelo wil spreken, die schepping van hemzelf, levert iets dat geen kunst, maar daarvan de parodie is. Wil het onbewuste kunstgevoel zich op het standpunt van het bewuste plaatsen, tracht een Javaan een eigen batik-ontwerp te maken, dan is het resultaat iets dat geen kunst, maar wansmaak te zien geeft: zijn leidraad ontvalt hem en hij is als een schip zonder roer in de stroomingen der kunst. De Javaan kan evenmin eenige eeuwen vooruit, als de Europeaan achterwaarts springen. Zooals thans de wajangverhalen bij den Javaan gemeengoed zijn, was het bij ons eens het Rolandslied; wij kunnen er niet naar terug. Iedere opzettelijke poging daartoe is tot falen gedoemd, omdat men zelfs met de beste bedoelingen geen kunst kan maken; geen individueele en geen gemeenschappelijke. Het is vergeefsche moeite geweest, dat Morris en zijn afschaduwingen ten onzent, Berlage en anderen, een nieuwe gemeenschapskunst hebben willen 'maken'.
terug naar de Inhoud

De geest schept de maat, niet de maat den geest
Met de maten van Grieksche godenbeelden kan men heden ten dage geen sculptuur maken die leeft, (66) met die van de Middeleeuwsche kunstnijverheid kon Morris geen nieuwe scheppen. De geest schept de maat, niet de maat den geest. Een bijna tragisch voorbeeld hiervan geeft ons Berlage te zien.
De tijd van de kathedraal van Ferrara, van de Perzische kunst en der Assyriërs was voor goed voorbij. De verhouding van gulden snede, van zijde tot diagonaal van het vierkant (1 : √2) die men in die antieke scheppingen terug kan vinden en toen den geest vermochten te bevruchten, zij hadden bij de Westersche kunst hun spankracht verloren.
Hooren wij naar hetgeen een van Berlage's medewerkers ons uit de praktijk van diens streven meedeelt: "Het meerendeel der architecten voelt niets voor 'schema's' en de overigen gebruiken ze niet, of, als zij ze toepassen, is het meer een probleem. Een typisch voorbeeld heb ik als teekenaar medegemaakt bij den Beursbouw. Berlage had speciale 'schema-driehoeken' laten maken met de rechthoekszijde 4 : 5, de z.g. Egyptische driehoek, door Viollet-le-Duc valschelijk (abusievelijk) zoo genoemd. Hiermede werd alles geteekend: details, het geometrische zoowel als het decoratieve ornament.
Toen ik aan het teekenen der gevels bezig was en de gegevens slechts in het schema waren te 'wringen', kwam Dr. Berlage te hulp. Hij zeide: "Als het niet gaat, doen wij het op het oog." Hiermede had hij gelijk en ongelijk. Ongelijk, omdat, indien het schema goed gekozen en goed gehanteerd kan worden, afwijken ervan niet toelaatbaar is. Gelijk, omdat het in de architectuur, als ruimtekunst, oneindig veel moeilijker is een ruimtelijk schema op te bouwen en door en door te kennen, dan dit in de muziek het geval is." (69) (Deze meening laten wij natuurlijk geheel voor rekening van den schrijver: J. d. M.).
"Missen wij in het schema dien leidsman, laat dan in hemelsnaam het kunstenaarsgevoel zoolang de leidsman blijven!" (Jan de Meyer, Bouwk. Weekblad Architectura, no. 31, 1 Aug. 1936).
Met andere woorden: ook aan Dr. Berlage gelukte het niet, kunst te construeeren. Egyptische driehoek en gulden snede waren dood. De tooverspreuk 'deed' het niet. Zelfs niet met wringen, en ondanks de nobele bedoeling.

En waarop berust dan dat 'kunstenaarsgevoel', zou men kunnen vragen? Als dit en niet het schema de leidsman moet zijn, wat is dan de waarde van het schema? Hebben wij er hier niet een voorbeeld van dat oude maten eens levenwekkende kracht bezaten, maar dat men er niets meer mee kan beginnen als de geest die ze bezielde niet meer aanwezig is? Dat dan, los van de oude maten, de persoonlijke inventie, gegrond op een persoonlijke 'snede', in hun plaats treedt? Zoo is dan de tegenstelling van blz. 51 verklaard en begrijpelijk, dat voor sommige gevallen en personen de oude verhoudingen levend bleven, dat zij niet de eenige schoonheidsnorm vormen, en sommigen de gulden snede als verouderd verwerpen. Nogmaals: de geest schept de maat, niet de maat den geest. (70)
Met andere woorden: de als goddelijk geprezen verhouding is dus niet anders dan de kristalliseering van een proportie-gevoel, berustend op een in de natuur vaak aangetroffen verhouding. Zonder dat levende gevoel vermogen de cijfers, waarin deze is vastgelegd, zoomin kunst te scheppen als de maat levend rhythme garandeert bij de muziek, of het aantal versvoeten levende poëzie bij de dichtkunst. En wie dat proportie-gevoel mist, of nog niet ontwikkeld heeft, vindt in de cijfers een ruggesteun die hem behoedt voor dwaze deraillementen. (71)
terug naar de Inhoud

Jan Poortenaar (bron: Wikipedia)
Jan Christiaan Poortenaar (Amsterdam, 23 juli 1886 - Naarden, 15 oktober 1958) was een Nederlandse graficus, grafisch ontwerper, kunstschilder, aquarellist, tekenaar, etser, lithograaf, vervaardiger van houtsnedes, illustrator, auteur en uitgever. Hij was autodidact, maar kreeg lessen van Piet van Wijngaerdt en Willem Witsen.
Jan Poortenaar kreeg op zijn 20e een Koninklijke Subsidie voor de Vrije Schilderkunst, en daarna volgden tentoonstellingen in Brussel en Londen. Van 1914 tot 1922 woonde Poortenaar in Londen, waar hij zijn eerste grote etsen maakte van Trafalgar Square, en de Waterloo Bridge. In 1915 won hij de zilveren medaille op de International Exhibition in San Francisco.

Poortenaar reisde veel, vergezeld door zijn vrouw Geertruida van Vladeracken (1880-1947) die zangeres, componiste en voordrachtskunstenares was. Hij begeleidde zijn vrouw op de piano op een reis door het toenmalige Nederlands-Indië, tussen 1922 en 1924. In Indië vond Poortenaar een overdaad aan onderwerpen. Terug in Nederland schreven zij een boek over 'Een kunstreis in de tropen'.
Hij werkte in Amsterdam, België, Londen tot 1922, Nederlands-Indië tot 1924, Bennekom (Ede), Amsterdam tot 1939 en Naarden van 1939 tot 1958. Hij vestigde zich in Naarden met de uitgeverij In Den Toren, waar hij tientallen boeken (meest van hemzelf) zou uitgeven.
Hij maakte landschappen, oriëntaalse voorstellingen, portretten, stadsgezichten, bloemen, stillevens, en exlibris. Hij schreef boeken met zijn eigen illustraties, vertaalde boeken en illustreerde andere boeken en tijdschriftartikelen.
Hij was lid van Arti et Amicitiae (Amsterdam) en de Haagse Kunstkring.
terug naar de Inhoud

Literatuur
Reinhold Bammes. Der Goldene Schnitt im Akzidengsatz. Archiv für Buchgewerbe, 1903. Heft 6.
Reinhold Bammes. Der Titelsatz. Monographien des Buchgewerbes, 1911. IV.
Ad. Beck. Die Proportionale Konstruktion der Geige. Leipzig, 1923.
H. P. Berlage. Grundlagen und Entwickelung der Architektur, vier Vortrage gehalten im Kunstgewerbemuseum zu Zürich. R'dam, zonder jaartal.
Sir Theodore Cook. The curves of life. London, 1914.
N. Altshiller Court. American Mathematical Monthly. 1917.
Dr. L.D. Caskey. Geometry of the Greek Vase. Yale University.
G. Dehio. Untersuchungen über das gleichseitige Dreieck als Norm gotischer Bauproportionen. Stuttgart, 1894.
A. Delaruelle. De gulden verhouding. Nova et Vetera, 1937-38.
Rud. Engel Hardt. Der Goldene Schnitt im Buchgewerbe. Leipzig - Reudnitz, 1919.
G.Th. Fechner, Vorschule der Aesthetik. 1897.
J. Probes, Lehrbuch der Experimentellen Psychologie. Herder en Co., Freiburg im Breisgau.
Dr. Ch. Funk-Hellet. Les oeuvres peints de la Renaissance italienne et le nombre d'or.
Dr. Adalbert Goeringer. Der Goldene Schnitt. München, 1e Aufl. 1893. 2e Aufl. 1911.
Matila C. Ghyka. Esthétique des proportions dans la nature et dans les arts. Gallimard, Paris.
Jay Hambridge. Dynamic symmetry, the Greek vase. Yale University Press, 1920.
H. Helmholtz. Die Lehre von den Tonempfindungen. Braunschweig 1862. 3e druk 1870. (72)

Alb. Hoffmann. Neue Grundsätze für die Anwendung der Proportionsgesetzes from Goldenen Schnitt auf den Buchdruck. Berlin, 1883. (Journal fur Buchdruckerkunst, Nr. 35-36).
Ernst Kapp. Grundlinien der Philosophie der Techniek. Braunschweig, 1877
J. Kübler. Die Proportionen des Goldenen Schnittes.
Dr. G. Mannoury. Mathesis en mystiek. Amsterdam, w. B. 1925.
Jan de Meyer. Bouwk. Weekblad Architecture. 1936. nrs. 13, 22, 31, 36, 43.
Max Möckel. Das Konstruktionsgeheimnis der alten italienischen Meister, der Goldene Schnitt im Geigenbau. Berlin, 1925.
Ernst Möckel. Vom Geheimnis der Form und der Urform des Seins. Stutt- gart-Berlin, 1938.
Ernst Mössel. Die Proportion in Antike und Mittelalter. München, 1926.
Luca Pacioli. De divina Proportione. Const. Winterberg. Wien, 1889.
F. Xav. Pfeifer. Der Goldene Schnitt im Mathematik, Natur und Kunst. Augsburg, 1885.
H.E. Timerding. Der Goldene Schnitt. Teubner, Berlin-Leipzig, 1919. 192;. (Math. Phys. Bibl. 1916).
Aug. Thiersch. Die Proportionen in der Architektur. Darmstadt, 1893.
J. Stuyt. Bouwkundige compositie. Antwerpen-Brussel, De Standaard Boekhandel.
Alex. Waldow. Handbuch der graphischen Künste. 1884.
Dr. Th. Wittstein. Der Goldene Schnitt und die Anwendung derselben in der Kunst, 1874.
G. Wolff, Mathematik und Malerei. Math. Phys. Bibl. 1916. Teubner, Berlin-Leipzig.
Th. Wolff. De Gulden Snede. W.A. Eisma, Leeuwarden, 1929.
A. Zeising. Neue Lehre von den Proportionen des menschlichen Körpers. Leipzig, 1854.
A. Zeising. Der Goldene Schnitt. Leipzig, 1858.

terug naar het literatuuroverzicht

terug naar het weblog






^