De tetraktys (viereenheid) van Pythagoras
De viereenheid
Het begrip tetraktys (Grieks: vierheid, groep van vier, viereenheid) stond in het middelpunt van de getallenleer van Pythagoras. Om tot de School der pythagoreeërs te worden toegelaten, moest een eed worden gezworen, die op de geestelijke betekenis van de Tetraktys wijst: "Ja, bij hem die onze geest de tetraktys gaf, die de wortels van de immer-stromende natuur bevat," en Pythagoras was degene die de tetraktys aan hen had overgedragen.
Pythagoras' tetraktys is de wiskundige aanwijzing voor het bestaan van het eeuwige leven: "de bron van de immer-stromende natuur."
De meetkunde
1. De tetraktys betekent 'vier-groep' en wordt op de eenvoudigste wijze gevormd door de eerste, eenvoudigste meetkundige vorm, de punt・, te vermenigvuldigen, want vermenigvuldiging is een van de wezenlijke eigenschappen van het leven. Daardoor ontstaan twee punten als de eenvoudigste volgende vorm, een lijn -- . Daardoor verschijnt de tweeheid, doordat ieder lijnstuk twee uiteinden, het ene en het andere heeft.
Wordt het lijnstuk, de eenheid van het ene en het andere, product van de eerste vermenigvuldiging, zelf voor de tweede keer vermenigvuldigd, dan ontstaat het gelijkbenige kruis ✕ , niet alleen doordat het tweede, andere lijnstuk alleen dan volkomen anders is als het dwars op het eerste lijnstuk staat, maar ook doordat ✕ het teken voor vermenigvuldiging is geworden (naast de punt・).
Door de vier uiteinden is het gelijkbenige kruis ✕ de meest eenvoudige weergave van Pythagoras' viergroep of vierheid: de tetraktys.
2. Het gelijkbenige kruis blijft een vorm in het platte vlak (twee-dimensionaal), maar de eerste vier getallen kunnen ook in een ruimtelijke vorm (drie-dimensionaal) worden weergegeven door de volgende meetkundige bewerking toe te passen:
de 1 wordt weergegeven door de op zichzelf staande punt, de zelfstandige eenheid,
de 2 door het lijnstuk dat de twee uiteinden, 1 en 2 (de twee zelfstandigheden aan de uiteinden van de lijn), tot een eenheid met elkaar verbindt,
de 3 door de gelijkzijdige driehoek, waarvan de tophoek het derde punt is, dat zich in het platte vlak naar de plaats tegenover het lijnstuk beweegt (de middelloodlijn) en die zich daardoor afstandelijk, maar evenwichtig tot de twee andere verhoudt, en
de 4 door de tetraëder, het viervlak, doordat het vierde punt in de ruimte vanuit de tophoek boven het middelpunt van de driehoek is gaan staan en die vanuit dat ene punt evenwichtig met de drie andere punten is verbonden, en daardoor de inwendige ruimte van de tetraëder vormt.
De rekenkunde als 'bron van de immer stromende natuur'
De tetraktys als de 'vier-groep' wordt ook gevormd door de eerste vier getallen uit de wiskundige verzameling van natuurlijke getallen: 1, 2, 3, 4 ... → ∞ . Deze verzameling zelf kan tot in het oneindige worden doorgeteld - 'de immer stromende natuur' - maar middels de gereduceerde cijfersom van de eerste vier getallen zijn ook die rekenkundig met die oneindigheid van de immer stromende natuur verbonden; immers, het optellen, door de gereduceerde cijfersom, van 1 + 2 + 3 + 4 geeft 10, dat ook opgeteld (1+0) weer 1 geeft, waardoor het viertal, de tetraktys weer van voren af aan begint en zich ten slotte in een kringloop tot in het oneindige vermenigvuldigt.
Het eerste viertal getallen bracht door optelling als het ware de tien voort, vandaar dat beide, zowel de tetraktys als de vierheid en de daaruit voortkomende tien, bij de pythagoreeërs volmaakt, heilig waren.
Uit deze vier eenvoudige meetkundige (punt, lijn, driehoek en viervlak) en rekenkundige grondeenheden (de vier eenvoudigste meetkundige vormen en de cijfers 1, 2, 3 en 4) is volgens Pythagoras zowel de geestelijke als de stoffelijke schepping voortgekomen, en worden die er ook eindeloos door voortgezet.
Datzelfde is ook het geval met het eerste zevental, dat opgeteld 28 geeft, dat opgeteld 2+8=10 en dat ook weer 1. Ook de zeven gold als een heilig getal.
De leerlingen van Pythagoras hadden geheimhouding beloofd en gaven de betekenis van de tetraktys niet door. Alleen Hiërokles, leider van de Alexandrijnse School in de vijfde eeuw, heeft er in het algemeen iets over gezegd.
Voor hem als pythagoreeër geldt: de Tetraktys is de godheid, bron van Eeuwige Orde.
De macht van tien is vier; want voor wij tot het volledige en volmaakte tiental komen, ontdekken wij al de deugd en volmaaktheid in de vier. Door de getallen van een tot vier samen te voegen, verkrijgen we tien. [zoals gezegd: de gereduceerde cijfersom: 1+2+3+4=10, 10 is 1+0=1]
De getallen van 1 t/m 10 kunnen op zinnebeeldige wijze worden weergegeven met ruimtelijke, stereometrische vormen: punt, lijn, driehoek, tetraëder, zesvlak, oktaëder, kubus en bol (zie 'Pythagoras' getallenleer'). Maar ook een reeks planimetrische figuren, de meetkunde in het platte vlak, figuren die uit elkaar voortkomen, voldoet geheel aan het begrip 'tetraktys' en aan de transcendente rekenkunde.
Het verschijnsel 'tetraktys' doet zich alleen voor dankzij de gereduceerde cijfersom of transcendente rekenkunde.
De achthoek als vorm van het getal 8 nog niet, maar de vormen van 9 en 10 beginnen steeds meer de volmaakte vorm van de cirkel te benaderen, met in de tienhoek het middelpunt als nieuwe 1.
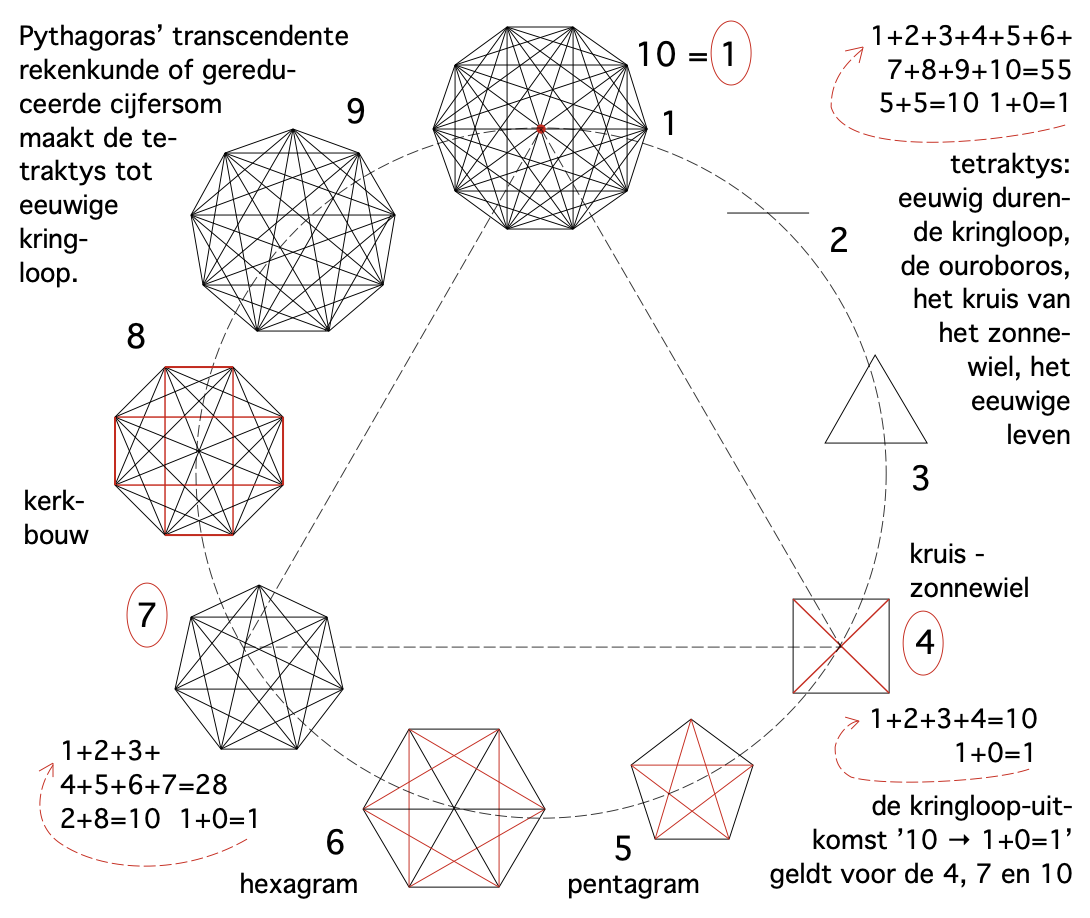
De tetraktys in het platte vlak is eveneens een toonbeeld van het eeuwige leven.
In rood bij 4 en 8 de kruisvorm +, zinnebeeld van het zonnewiel: de eeuwige kringloop.
Vier is een rekenkundig gemiddelde tussen één en zeven, en dit getal is drie, daar vier evenveel meer dan één is als zeven meer dan vier [zie de afbeelding].
De eenvoud en het zevenvoud
De vermogens en eigenschappen van de eenheid en van het zevenvoud zijn zeer groot en uitmuntend, want als principe van alle getallen bevat de eenheid de vermogens van alle. Daar de zeven een 'maagd' is en geen 'moeder' heeft, behoudt zij ook de deugd en de volmaaktheid van de eenheid: zij wordt niet door een ander getal in de reeks van één tot tien verwekt en brengt binnen die reeks ook geen ander getal voort... Bovendien zijn er vier vermogens die de dingen beoordelen: zintuigelijke waarneming, kennis, begrip en mening [het Griekse 'logos'-begrip].
In één woord: de Tetraktys bevat alle vormen van begin tot einde en verbindt ze met elkaar: de elementen, de getallen, de jaargetijden, de tijdperken, de maatschappijen en de gemeenschappen... De goddelijke Tetraktys is nu [volgens Hiërocles] zo ver beschreven als de ons opgelegde grenzen toelaten.

tetraktys
Het gelijkbenige kruis staat in het middelpunt van de zinnebeelden die Jezus' leer van het eeuwige leven van het koninkrijk Gods weergeven (zie de 'viereenheid of quaterniteit' in het Menu).
Het vierkant speelt een doorslaggevende rol in het bewijs van de Stelling van Pythagoras.
Deze stelling is: in een rechthoekige driehoek met zijden a, b en c is de som van het kwadraat van de rechthoekszijden a en b gelijk aan het kwadraat van de schuine zijde c.
Meetkundig bewijs:
Teken om de driehoek abc de vierkanten die het kwadraat van de zijden weergeven: a², b² en c².
Teken vervolgens een vierkant met zijden a+b en teken daarin de driehoek abc.
Vanuit de hoekpunten van de driehoek kan het vierkant worden verdeeld en twee vierhoeken a² en b²; in het overblijvende oppervlak kunnen 4 driehoeken abc worden getekend.
Teken een tweede vierkant met zijden a+b en daarin vier maal de driehoek abc, maar vanuit de vier hoekpunten. Wat overblijft is het vierkant c².
Van het oppervlak van beide vierkanten met zijden a+b zijn 4 driehoeken abc afgetrokken, waardoor de overblijvende oppervlakten gelijk zijn, m.a.w. a² + b² = c².
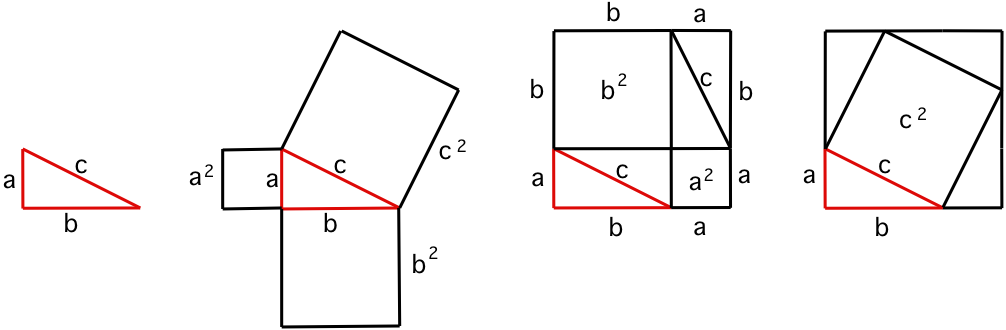
Het eerste stel cijfers als oplossing van de vergelijking a² + b² = c² is: 3, 4 en 5.
Rekenkunde en het magische getal vier
1) Van de natuurlijke getallen is het getal 4 als eerste een z.g.n. 'samengesteld getal', d.w.z. een getal met echte delers: een heel getal, groter dan 1, maar kleiner dan het bewuste getal zelf.
Immers, in dat geval is de eerst mogelijke van alle delingen: 4 : 2 = 2.
2) De vergelijking ab = ba
Omdat 2 x 2 = 2² is het getal 2 een oplossing van de vergelijkingen 2a = a² en 2a = 2a. Beide zijn een bijzonder geval van de bijzondere vergelijking ab = ba.
Als je b = a neemt, is deze vergelijking waar voor elke a. Maar wat zijn de andere oplossingen? De wiskundige Euler bewees dat deze vergelijking slechts één oplossing heeft, als je aanneemt dat a en b gehele getallen zijn en 0 < a < b. Namelijk: 4²=24= 16 [en vlgs Pythagoras’ cijfersom is 1+6=7].

Babylonische meetkunde
In Babylon kwam Pythagoras in aanraking met babylonische meetkundige figuren, zoals op dit kleitablet is te zien: vierkanten en sommige met diagonalen.
Een vierkant heeft vier zijden. Wat is de lengte van de zijden als oppervlakte en omtrek gelijk zijn?
Noem de lengte van de zijden a. Dan is de omtrek 4a en de oppervlakte a². Willen deze aan elkaar gelijk zijn, dan moet gelden dat a² = 4a. Als we deze vergelijking oplossen krijgen we: a (a - 4) = 0, zodat de oplossingen zijn: a = 0 of a = 4.
De eerste oplossing is een vierkant zonder afmetingen. De tweede oplossing a = 4 geeft een vierkant met zijde 4. Een vierkant waarvan de oppervlakte gelijk is aan de omtrek heeft zijde 4! [4x4=16 en 1+6=7]

magisch vierkant
In dit vierkant zijn de getallen 1 t/m 16 zodanig geplaatst, dat de som van de getallen in elke rij, kolom of diagonaal, gelijk is. Dit vierkant (er zijn er meer) verwijst naar het intellect [het ingekeerde denken vanwege het getal 7].
De som van de getallen in elke rij, kolom of diagonaal is steeds gelijk aan 34 [3+4=7], de magische constante genoemd. Maar er is nog meer bijzonders aan de hand:
- de vier hoekpunten 16,13,1 en 4 hebben 34 als som
- de vier getallen in het centrum 10,11,7 en 6 hebben 34 als som
- de 3 en 2 in de bovenste rij en de 15 en 14 in de onderste hebben 34 als som
- de 5 en 9 in de eerste kolom en de 8 en 12 in de laatste hebben 34 als som
- kloksgewijs rondgaande rond het centrum en het optellen van de getallen 3,8,14 en 9 naast de hoekpunten, geeft ook 34 en hetzelfde voor de getallen 5,2,12 en 15 ook 34
- de getallen naast de diagonaal tegenover liggende hoekpunten 3,5,12 en 14 en 2,8,9 en 15 opgeteld 34 [i.v.m. de 4 van het vierkant en de 7 van 3+4, is vlgs Pythagoras niet alleen 1+2+3+4=10, maar ook 1+2+3+4+5+6+7=28 en 2+8=10]
5) Vier temperamenten
In de middeleeuwen geloofde men dat alles opgebouwd was uit vier 'elementen': aarde, water, lucht en vuur. Het karakter van de mens [de geest] werd ingedeeld volgens vier bijbehorende temperamenten.
aarde [waarn.] melancholisch (zwaarmoedig)
water [voelen] flegmatisch (gelijkmoedig)
lucht [denken] sanguinisch (warmbloedig)
vuur [willen] cholerisch (opvliegend)
Bron 1), 2), 3), 4), 5): Pythagoras, Wiskundetijdschrift juni 2001

de kwadratuur
van de cirkel
De omtrek van een cirkel met straal r kan worden berekend met de formule: 2πr, terwijl de omtrek van een vierkant met zijde a is: 4a.
Voor de oppervlakte van een cirkel met straal r is de formule πr² en de oppervlakte van een vierkant met zijde a is: a x a of a². Om het oppervlak van een cirkel te berekenen, moet dus een 'kwadraat', dat is een vierkant worden gebruikt. Maar terwijl het oppervlak van het vierkant eenvoudig a x a is, waarvoor natuurlijke, rationele getallen worden gebruikt, moet voor het oppervlak van een církel het getal π worden gebruikt: 3,14… → ∞, wat een zich in het oneindige voortzettende breuk is, die daardoor een irrationeel, nooit tot een einde komend getal oplevert; en datzelfde geldt voor de omtrek van een cirkel.
De vastliggende ómtrek van dat bewuste vierkant (want door een natuurlijk getal) kan niet gelijk zijn aan de niet vastliggende omtrek van die cirkel (want door een irrationeel getal) (zie afbeelding) en datzelfde geldt voor hun oppervlakken (want rationele én irrationele, nooit eindigende breuken als 'getal')!
Het getal π is een breuk waarvan de deling oneindig doorgaat en is daardoor een transcendent, in feite een onbekend, want nooit eindigend 'getal'; het is een getal dat een benadering is, een 'ongeveer', het getal is zich niet voor te stellen; terwijl de omtrek van het vierkant een geheel, natuurlijk getal is.
Daarnaast heeft een cirkel geen einde of begin en is daardoor een zinnebeeld voor de oneindigheid, terwijl een vierkant met een passer of een meetlat is te vormen, waardoor de afmetingen daarvan bekend zijn; een vierkant behoort daardoor tot de aarde, de stoffelijke schepping.
De tetraktys heeft beide eigenschapen in zich, want als viergroep is het een vierkant, maar als de rij 1,2,3,4 en als de cijfersom daarvan: 1+2+3+4=10 en 1+0=1 is het een cirkel, doordat het einde, de 10, naar het begin van de rij, de 1, terugverwijst.
De toonladder
Pythagoras ontwikkelde proefondervindelijk (m.b.v. het monochord) het octaaf en ontdekte daarbij de harmonische samenklanken kwart, kwint en octaaf, de verhouding van twee noten die goed samenklinken. De verhoudingen daarvoor waren 4:3, 3:2 en 2:1. Zij konden dus worden uitgedrukt met de vier getallen van de tetraktys, waardoor zijn muziekleer daar ook mee samenhing.
De verhoudingen 2:1, 3:2 en 4:3 worden weergegeven door de vier lagen van punten van de tetraktys.
Het gezin
Pythagoras' 'vier-groep' of viereenheid kan op meerdere wijzen worden uitgedrukt.
In de tetraëder heeft iedere zijde een gelijkwaardige zijde tegenover zich, maar die wel haaks op die zijde staat. Als de tetraëder als samengesteld lijnstuk op een van de zijden wordt bezien, wordt in het platte vlak een vierkant met diagonalen zichtbaar.
In het vierkant lopen alle tegenoverstaande zijden wel evenwijdig, maar zijn omgekeerden van elkaar: 1 → 2 gaat naar rechts en 3 → 4 naar links. Zo zijn alle hoekpunten op evenwichtige wijze met elkaar te verbinden: de toestand binnen het gezin als vader en moeder, zoon en dochter: een, twee, drie en vier, Pythagoras' heilige tetraktys of viereenheid als het gezin - dat bij Pythagoras in hoog aanzien stond.
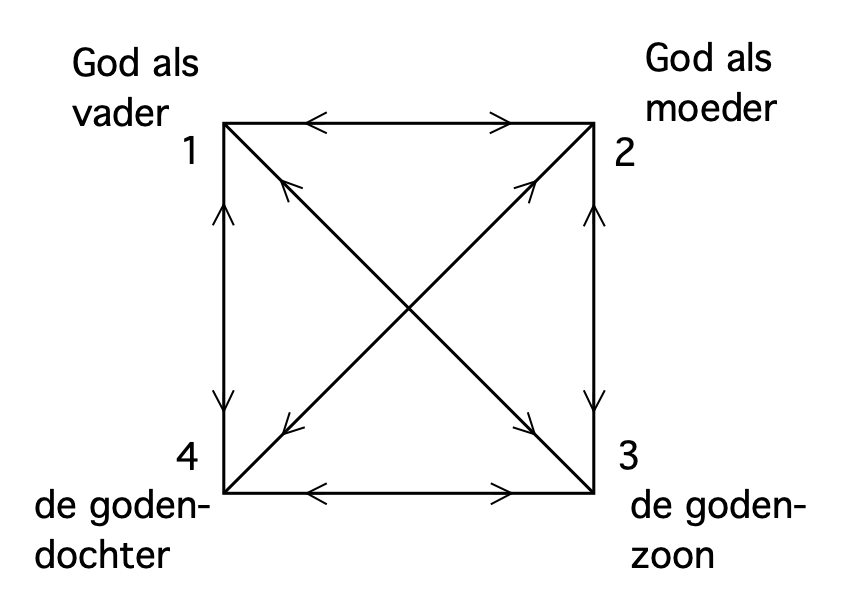
goddelijk gezin
Dit vierkant beschrijft ook de werkelijkheid van de godheid in de vorm van het oergezin: de verhouding tussen een, twee, drie en vier, die in het gezin een hechte eenheid vormen doordat de zoon en de dochter uit de vader en de moeder zijn voortgekomen als een nieuwe schepping, als een paar dat een voortzetting is van henzelf.
Dit gezin gaat zich vervolgens eindeloos herhalen doordat op een + twee de drie + vier volgen, wat samen gelijk is aan tien: het einde en het nieuwe begin in de vorm van de een.
Zo worden in de godheid steeds nieuwe gezinnen gevormd.
Met andere woorden: punt 1, lijnstuk 2 (verbinding 1 en 2), driehoek 3 (verbinding 1, 2 en 3) en tetraëder 4 laten zien, dat de 4 tenslotte de verbinding is van 1, 2 en 3. Die verbinding wordt ruimtelijk weergegeven door de tetraëder en in het platte vlak door het vierkant, een gelijkzijdige vierhoek met twee diagonalen, die - volgend op de drie met zijn gelijkzijdige driehoek - daarmee een begrijpelijke samenhang heeft en als vierkant op eenvoudige, natuurlijke wijze het vervolg is van de gelijkzijdige driehoek.
In het Oud-Grieks (Koinè):
tetra-ktys: viergroep 1+2+3+4=10
tetra-gonos: vierhoekig, vierkant, sterk, volmaakt
(Oudnederlands 'deugd': goed zijn, krachtig zijn, passend zijn
Ergens vierkant achter staan: iets volledig beamen.)
De kern van de tetraktys was volgens Pythagoras' getallenleer: 1+2+3+4=10, en 1+0=1
De laatste een wijst weer terug naar de eerste, waardoor de kringloop is gesloten.
De vorm werd op meerdere manieren weergegeven.
Het voorkomen van de viereenheid
kruis in cirkel
de vier windrichtingen: de windroos Noord, Oost, Zuid en West;
de vier elementen: aarde, water, lucht en vuur;
de vier kwaliteiten: warm en koud, vochtig en droog;
de vier jaargetijden: lente, zomer, herfst en winter;
de vier dagdelen: ochtend, namiddag, avond en nacht.
de vier schijngestalten van de maan.
Bij de mens in de vorm van het gezin als vader, moeder, zoon en dochter;
als de vier vermogens: waarnemen, denken, voelen en willen;
de vier temperamenten: flegmatisch, cholerisch, sanguinisch en melancholisch;
de vier complementaire kleuren: rood en groen, geel en blauw;
in de natuurkunde als de drie dimensies van de ruimte en de tijd als vierde.
Bij het getal 4 is ook sprake van een bijzondere eigenschap door een harmonie van rekenkundige bewerkingen, die bij geen ander getal voorkomt: 2+2=4, 4-2=2, 2x2=4, 4:2=2 en 2 tot de 2e macht (kwadraat) is een vierkant: 4. De vier vormt als zodanig de afsluiting van een ontwikkeling die aan de hand van de getallen 1,2,3,4 wordt uitgebeeld, waarbij God de één is, die schept in tweevoud en waarbij de mens op aarde de derde stap maakt, die bij de vierde stap door bezinning op zichzelf de mogelijkheid heeft zich weer met de 1 te verbinden. Want al het andere dat nog moet komen, vloeit uit deze vier voort en de vier heeft het vermogen in zich van de tien: 1+2+3+4=10 en de tien weer van de 1: 1+0=1, wat het doel is: de hereniging.
Door de zelfbezinning van de vier kan de mens weer tot zichzelf komen en zich van daaruit innerlijk op zijn oorsprong gaan richten.
Het Oude Testament
De vier dieren in het visioen van Ezechiël: rund, leeuw, adelaar en mens;
met ieder vier vleugels en vier gezichten
de vier evangelisten: Markus, Mattheüs, Lukas en Johannes;
de vier rivieren in het paradijs, die uit de ene hoofdrivier voortkomen (Genesis);
De naam van God is Iehovah (de vijf klinkers i, e, o, u, a) →
als IHVH, י ה ו ה het tetragrammaton.
Alchemie
De alchemie was een wedergeboorte van de Griekse filosofie en daarmee ook van Pythagoras. In de alchemie ging het om de elementen en de eigenschappen:
water en vuur - aarde en lucht
warm en koud - droog en vochtig (ook zij vormen ieder een kruis)
De alchemie wordt gekenmerkt door een geestelijke ontwikkelingsweg, een transformatie of omvorming, die op de scheikundige omvormingen, die in hun retorten plaatsvonden, werd overgedragen. Het ging om een scheikundige scheiding van stoffen en een vereniging van stoffen, waarbij 'het ene' in vier delen is te verdelen. In die omvorming van stoffen herkenden zij bewust of onbewust een geestelijk gebeuren: de zelfverwerkelijking.
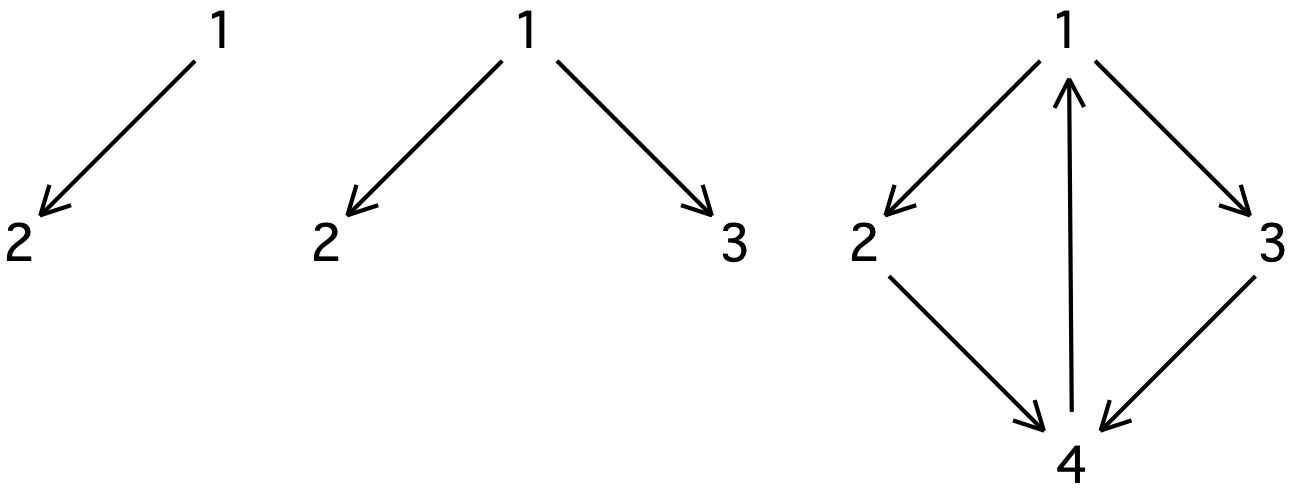
Axioma van Maria
Dit beschrijft het verloop van een zogenaamde scheikundige evenwichtsreactie, die in de natuur veel voorkomt: De uitgangsstof (1) wordt gescheiden in de beide samenstellende stoffen (2 en 3) die weer met elkaar kunnen reageren (4) tot een eenheid (1).
Genetica
De tetraktys of 'groep van vier' komt ook voor in de biologie en wel in het vakgebied genetica. Daar vormt een groep van vier 'nucleobasen' (of purinebasen) de zogenaamde 'codonen'.
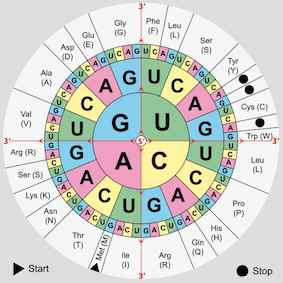
nucleobasen, codonen en aminozuren
De 'groep van vier' nucleobasen zijn:
Adenine, Thymine (of Uracil in RNA), Guanine en Cytosine (A, T, G (of U) en C).
Alle levensvormen op aarde gebruiken deze genetische code; dat is een belangrijke aanwijzing dat alle levensvormen van één gemeenschappelijke voorouder afstammen. Deze wetenschappelijke bevinding bevestigt voor de levensvormen op aarde een van Pythagoras' stellingen, dat alles uit één bron afkomstig is en dat daardoor alles met elkaar samenhangt.
En middels de vier nucleobasen hangt die uitspraak ook samen met de tetraktys.
Zoals de tetraktys aan het begin staat van de eindeloze rij van getallen, zo staan de vier nucleobasen aan het begin van een schier eindeloze reeks van levensvormen op aarde.
Klik hier voor een wetenschappelijk artikel over dit onderwerp.
terug naar Pythagoras' getallenleer
terug naar God als man en vrouw
terug naar de viereenheid of quaterniteit
terug naar de woordenlijst T
terug naar het weblog
^