De vierheid in de meetkunde
In de meetkunde berusten een aantal belangrijke meetkundige figuren op de vierheid.
De cirkel heeft één paar middellijnen die samen een gelijkbenig kruis vormen.

De bol heeft drie paar middellijnen die ieder een gelijkbenig kruis vormen.

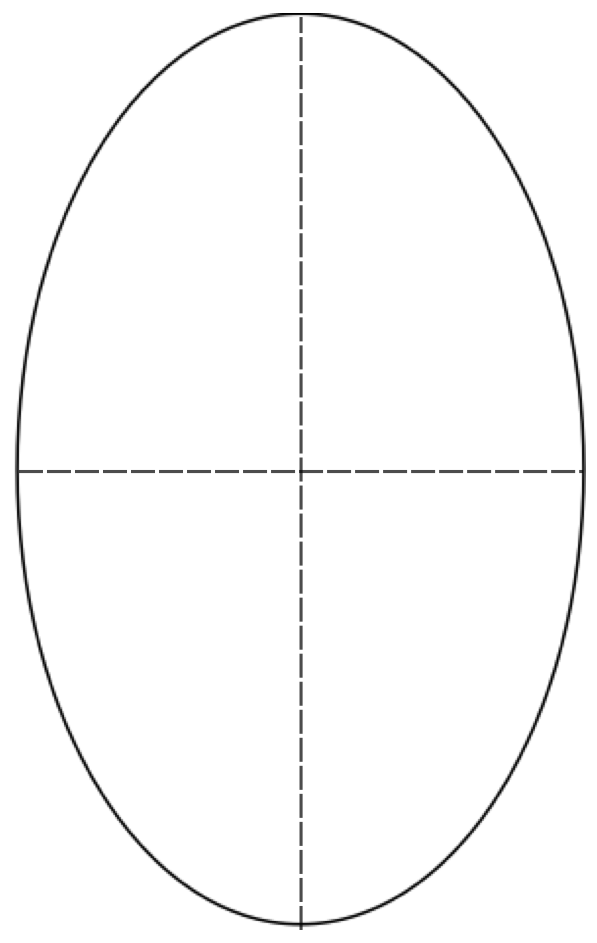
De ellips heeft twee middellijnen die samen een ongelijkbenig kruis vormen, dat de vorm heeft van de levensboom.
Het vierkant heeft één paar diagonalen, die samen een gelijkbenig kruis vormen.

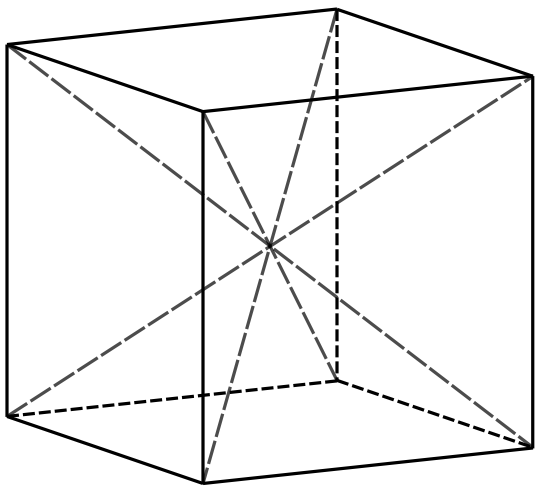
De kubus met de vier ingetekende diagonalen; de beide paren vormen ieder een gelijkbenig kruis. De diagonalen van de zijvlakken zijn niet getekend, maar zij vormen zes gelijkbenige kruisen.
Toevoeging:
In zijn boek 'Meno' (een Sokratische dialoog) stelde Plato de vraag naar de 'verdubbeling van het vierkant', waarbij hij Sokrates aan een jongen laat aantonen, hoe hij door middel van sokratische vragen zelf tot de oplossing kan komen. Het probleem, ook bekend als het 'delische probleem', betrof het verdubbelen van de oppervlakte van een vierkant, met behulp van de diagonaal ervan.
Scientias.nl meldt hierover het verslag van een onderzoek, hoe ChatGPT deze vraag beantwoordde.
ChatGPT gaat eerst de mist in met een oud wiskundig raadsel. Maar dan verrast het de onderzoekers
Scientias, Jeannette Kras, 20 september 2025
ChatGPT is net een middelbare scholier: ook hij snapt in eerste instantie weinig van een oud wiskundeprobleem. En ook hij komt met een beetje improviseren en trial en error een heel eind, blijkt uit nieuw Brits onderzoek.
Maar de chatbot is niet zomaar dom aan het stuntelen. Hij wist de Cambridge-onderzoekers al snel te verrassen met zijn improvisatiestijl. Het experiment draait om het klassieke vraagstuk van het 'verdubbelen van het vierkant', beschreven door Plato rond 385 voor Christus. In die dialoog laat Socrates een jongen nadenken over hoe je de oppervlakte van een vierkant verdubbelt. Eerst denkt de jongen dat je simpelweg de zijden moet verdubbelen, maar Socrates leidt hem naar de juiste oplossing: gebruik de diagonaal van het oorspronkelijke vierkant als nieuwe zijde.
Het eerste vierkant met ribbe 1 heeft een oppervlak 1. Dat vierkant heeft een diagonaal; het oppervlak van het daarmee gevormde tweede vierkant is 2x zo groot als het eerste.
De diagonaal is √2. Het tweede oppervlak is (√2)2 = 2
De diagonaal is √2. Het tweede oppervlak is (√2)2 = 2

ChatGPT's aanpak
De onderzoekers vroegen ChatGPT-4 het raadsel van Plato op te lossen. Ze verwachtten dat de chatbot direct Plato's bekende antwoord zou reproduceren. Maar tot hun verbazing gingen de gedachtenkronkels van de AI een heel andere kant op. "Wanneer we voor een nieuw probleem staan, is onze eerste neiging vaak om dingen uit te proberen op basis van eerdere ervaring," zegt onderzoeker Nadav Marco. "In ons experiment leek ChatGPT iets vergelijkbaars te doen. Als een leerling kwam het zelf met hypotheses en oplossingen."
In plaats van naar geometrie te grijpen, koos ChatGPT voor algebra. Dat bestond in Plato's tijd nog helemaal niet. Toen de onderzoekers het AI-model richting de foutieve denkwijze van de jongen lieten denken, hield de chatbot toch koppig vast aan zijn algebraïsche redeneringen. Pas toen de onderzoekers hun teleurstelling uitten dat het geen "elegant en exact" antwoord kon geven, schakelde ChatGPT alsnog over naar de geometrische oplossing.
Hardnekkige voorkeur voor algebra
Ook bij varianten van de puzzel, zoals het verdubbelen van een rechthoek of een driehoek, koos de chatbot in eerste instantie voor een algebraïsche aanpak. Toen het bij de rechthoek zelfs foutief beweerde dat een geometrische oplossing onmogelijk was, zagen de onderzoekers iets opvallends. "De kans dat dit verkeerde antwoord rechtstreeks uit de kennisbasis van het model kwam, is verwaarloosbaar", legt Marco uit. "Het leek zijn reacties ter plekke te improviseren, beïnvloed door ons eerdere gesprek over het vierkant." Bij de driehoek hield de AI wederom eerst vast aan algebra, maar vond het na wat aanmoediging van de onderzoekers uiteindelijk toch de juiste geometrische aanpak.
Digitale leerling
Het team wijst erop dat ChatGPT geen mens is en niet 'denkt' zoals wij dat doen, maar ze noemen zijn gedrag toch 'leerlingachtig'. "Als het puur informatie uit zijn geheugen had opgehaald, zou het vrijwel zeker meteen naar de klassieke oplossing met de diagonaal hebben verwezen. In plaats daarvan leek het zijn eigen route te nemen," vertelt hoofdonderzoeker Andreas Stylianides. Dit doet denken aan het onderwijskundige concept van de 'zone van naaste ontwikkeling', een concept van Lev Vygotsky dat het verschil beschrijft tussen wat een kind of leerling zelfstandig kan en wat het kan bereiken met hulp of begeleiding van een meer bekwame persoon, zoals een volwassene of oudere medeleerling. Misschien, zo speculeren de onderzoekers, heeft AI een soortgelijke zone.
De conclusie die het Cambridge-team trekt is tweeledig. Enerzijds laat het experiment zien dat ChatGPT niet altijd betrouwbaar is in de wiskundige bewijsvoering. Anderzijds is dat juist een kans om verder te komen. "In plaats van te vragen: geef me het antwoord, kun je ChatGPT beter vragen: laten we dit probleem samen verkennen," besluit Marco.
Of zoals Stylianides samenvat: "Studenten kunnen niet zomaar aannemen dat de bewijzen die ChatGPT aandraagt honderd procent kloppen. Het kritisch begrijpen en evalueren van AI-bewijzen is vanaf nu een essentiële vaardigheid in het wiskundeonderwijs."
Bron:
"An exploration into the nature of ChatGPT's mathematical knowledge" - International Journal of Mathematical Education in Science and Technology
Inhoud van de dialoog:
Context: Het vraagstuk komt ter sprake als Socrates het concept van deugd (aretè) probeert te definiëren, maar er niet in slaagt een eenduidige definitie te geven.
Socratische methode: Socrates stelt een reeks doordachte vragen aan een ongeschoolde jongen om hem via de rede en het herinneren van kennis (anamnese) tot de correcte oplossing te leiden.
De oplossing: De jongen ontdekt dat om het vierkant te verdubbelen, de zijden van het vierkant met de wortel uit twee vermenigvuldigd moeten worden, wat leidt tot de ontdekking van de irrationaliteit van de wortel uit twee.
Betekenis:
De discussie in de Meno illustreert Plato's opvatting dat kennis niet geleerd wordt, maar een herinnering is van reeds bestaande kennis in de geest. De dialoog demonstreert zo het principe van anamnese en het vermogen van de geest om door middel van rationele reflectie tot ware kennis te komen.
Meno (Plato) - (Wikipedia) De Meno is een van de socratische dialogen van Plato, waarschijnlijk tussen 386 en 382 v.Chr. geschreven. Dit werk markeert een keerpunt in Plato's filosofische ontwikkeling: daar waar zijn eerdere werken puur 'aporetisch' (dat wil zeggen in een aporie, een situatie zonder antwoord) eindigden, wordt in de Meno een nieuwe bron van zekere kennis aangeboord. Als de gesprekspartners er nl. niet in slagen te definiëren wat aretè is ('voortreffelijkheid' of 'deugd', een brede term, hier vooral op de politiek toegepast), wordt de vraag gesteld of wij überhaupt wel iets kunnen leren.
Plato's antwoord op deze vraag kan gezien worden als het eerste optreden binnen de westerse filosofie van het idee van de aangeboren kennis. Plato zegt namelijk dat onze kennis in feite een herinneren is van eerder bezeten kennis, een opvatting die bekend is geworden onder de naam anamnese.
terug naar het overzicht
terug naar het weblog
^